
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)

科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=70°,∠B=60°,∠ACD是△ABC的一个外角,∠ACD的度数为( )
A. 50° B. 60° C. 70° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三条边的长分别为3、4、5,与△ABC相似的△A′B′C′的最长边为15.则△A′B′C′最短边的长为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile 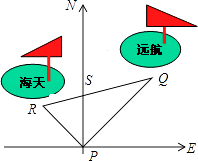
(1)求PQ,PR的长度;
(2)如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,动点
中,动点![]() 从
从![]() 出发,沿
出发,沿![]() 方向运动,当点
方向运动,当点![]() 到达点
到达点![]() 时停止运动,过点
时停止运动,过点![]() 做
做![]() ,交
,交![]() 于
于![]() 点,设点
点,设点![]() 运动路程为
运动路程为![]() ,
,![]() ,如图2所表示的是
,如图2所表示的是![]() 与
与![]() 的函数关系的大致图象,当点
的函数关系的大致图象,当点![]() 在
在![]() 上运动时,
上运动时,![]() 的最大长度是
的最大长度是![]() ,则矩形
,则矩形![]() 的面积是( )
的面积是( )
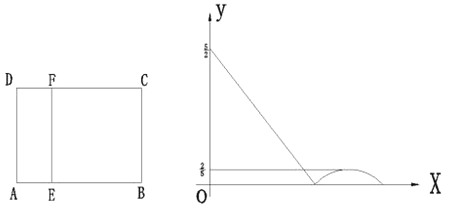
图1 图2
A.![]() B.
B.![]() C.6 D.
C.6 D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com