
【题目】如图,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于点B,且四边形BCOE是平行四边形。
(1)BC是⊙O的切线吗?若是,给出证明:若不是,请说明理由;
(2)若⊙O半径为1,求AD的长。
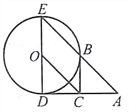
【答案】(1)是切线, 证明见解析;(2)2
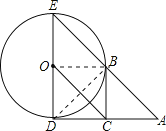
【解析】试题分析:(1)连接OB,由BC与OD平行,BC=OD,得到四边形BCDO为平行四边形,由AD为圆的切线,利用切线的性质得到OD垂直于AD,可得出四边形BCDO为矩形,利用矩形的性质得到OB垂直于BC,即可得出BC为圆O的切线.
(2)连接BD,由ED为圆O的直径,利用直径所对的圆周角为直角得到∠DBE为直角,由BCOE为平行四边形,得到BC与OE平行,且BC=OE=1,在直角三角形ABD中,C为AD的中点,利用斜边上的中线等于斜边的一半求出AD的长即可.
试题解析:解:(1)是.理由如下:
如图,连接OB.∵BC∥OD,BC=OD,∴四边形BCDO为平行四边形.∵AD为圆O的切线,∴OD⊥AD,∴四边形BCDO为矩形,∴OB⊥BC,则BC为圆O的切线.
(2)连接BD.∵DE是直径,∴∠DBE=90°.∵四边形BCOE为平行四边形,∴BC∥OE,BC=OE=1.在Rt△ABD中,C为AD的中点,∴BC=![]() AD=1,则AD=2.
AD=1,则AD=2.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.
(1)求抛物线的解析式;
(2)过点A的直线交直线BC于点M.
①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 30 | 42 |
租金/(元/辆) | 300 | 400 |
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )
图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )
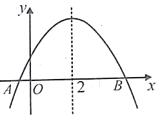
A. ①,② B. ②,③ C. ③,④ D. ②,④
查看答案和解析>>
科目:初中数学 来源: 题型:
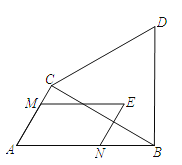
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=6,△BCD为等边三角形,点E为△BCD围成的区域(包括各边)内的一点,过点E作EM∥AB,交直线AC于点M,作EN∥AC,交直线AB于点N,则![]() 的最大值为_____.
的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
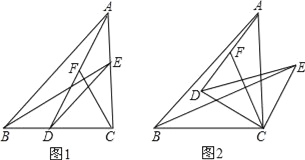
【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则满足下列条件的一定是直角三角形的是( )
A. ∠A:∠B:∠C=3:4:5B. a:b:c=1:![]() :3
:3
C. a=7,b=24,c=25D. a=32,b=42,c=52
查看答案和解析>>
科目:初中数学 来源: 题型:
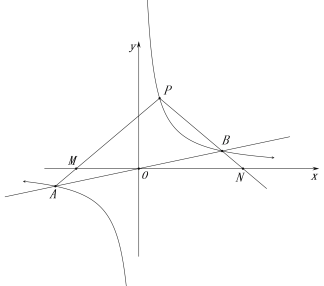
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)求k的值;
(2)设直线PA,PB与x轴分别交于点M,N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P,B之间的动点(与点P,B不重合),连接AQ,BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com