
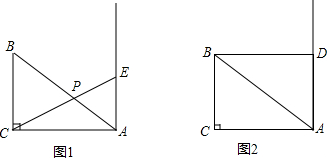
 ��ͼ����ABC�У���ACB=90�㣬BC=6��AC=8����E���B��AC��ͬ�࣬��AE��AC��
��ͼ����ABC�У���ACB=90�㣬BC=6��AC=8����E���B��AC��ͬ�࣬��AE��AC������ ��1����AE��AC����ACB=90�㣬�ɵ�AE��BC��Ȼ����ƽ���߷��߶γɱ������������y����x�ĺ�������ʽ��
��2����������Ҫʹ��PAE���ABC���ƣ�ֻ�С�EPA=90�㣬��CE��AB��Ȼ���ɡ�ABC�ס�EAC����ô𰸣�
��3���õ�C���ڡ�E�ⲿ����ʱ��C����E�ϵ�ľ������СֵΪCE-DE��Ȼ��ֱ�ӵ���E���߶�AD��ʱ�뵱��E���߶�AD�ӳ�����ʱ��ȥ������⼴����ô𰸣�
��� �⣺��1����AE��AC����ACB=90�㣬
��AE��BC��
��$\frac{AE}{BC}$=$\frac{AP}{BP}$��
��BC=6��AC=8��
��AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=10��
��AE=x��AP=y��
��$\frac{x}{6}$=$\frac{y}{10-y}$��
��y=$\frac{10x}{x+6}$��x��0����
��2���ߡ�ACB=90�㣬����PAE���PEA������ǣ�
��Ҫʹ��PAE���ABC���ƣ�ֻ�С�EPA=90�㣬��CE��AB��
��ʱ��ABC�ס�EAC����$\frac{AE}{8}$=$\frac{8}{6}$��
��AE=$\frac{32}{3}$��
�ʴ��ڵ�E��ʹ��ABC�ס�EAP����ʱAE=$\frac{32}{3}$��
��3���ߵ�C���ڡ�E�ⲿ��
���ʱ��C����E�ϵ�ľ������СֵΪCE-DE��
��AE=x��
�ٵ���E���߶�AD��ʱ��ED=6-x��EC=6-x+8=14-x��
��x2+82=��14-x��2��
��ã�x=$\frac{33}{7}$��
����E�İ뾶Ϊ$\frac{9}{7}$��
�ڵ���E���߶�AD�ӳ�����ʱ��ED=x-6��EC=x-6+8=x+2��
��x2+82=��x+2��2��
��ã�x=15��
����E�İ뾶Ϊ9��
���E�İ뾶Ϊ9��$\frac{9}{7}$��
���� ��������Բ���ۺ��⣮���������������ε��ж������ʡ����ߵ������Լ����ɶ�����֪ʶ��ע�����շ�������˼���Ӧ���ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
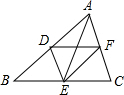 ��ͼ��D��E��F�ֱ��ǡ�ABC�ı�AB��BC��AC���е㣮���ı���ADEF�����Σ����ABC��������������ǣ�������
��ͼ��D��E��F�ֱ��ǡ�ABC�ı�AB��BC��AC���е㣮���ı���ADEF�����Σ����ABC��������������ǣ�������| A�� | AB��AC | B�� | AB=AC | C�� | AB=BC | D�� | AC=BC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 2 | C�� | $\sqrt{3}$ | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�������������Ͻ���ֱ������ϵxOy��ʹ������λ�ڵ㣨-1��-2�������R��λ�ڵ㣨2��-2�������ڡ�λ�ڵ㣨������
��ͼ�������������Ͻ���ֱ������ϵxOy��ʹ������λ�ڵ㣨-1��-2�������R��λ�ڵ㣨2��-2�������ڡ�λ�ڵ㣨������| A�� | ��-2��-1�� | B�� | ��0��0�� | C�� | ��1��-2�� | D�� | ��-1��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com