
分析 (1)令x+y=a,x-y=b,原方程变形为$\left\{\begin{array}{l}{3a-4b=4}&{①}\\{3a+b=6}&{②}\end{array}\right.$,解之求得a、b的值,即可得$\left\{\begin{array}{l}{x+y=\frac{28}{15}}\\{x-y=\frac{2}{5}}\end{array}\right.$,进一步解之可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)令x+y=a,x-y=b,
则原方程变形为$\left\{\begin{array}{l}{3a-4b=4}\\{\frac{a}{2}+\frac{b}{6}=1}\end{array}\right.$,整理,得:$\left\{\begin{array}{l}{3a-4b=4}&{①}\\{3a+b=6}&{②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{28}{15}}\\{b=\frac{2}{5}}\end{array}\right.$,即$\left\{\begin{array}{l}{x+y=\frac{28}{15}}\\{x-y=\frac{2}{5}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{17}{15}}\\{y=\frac{11}{15}}\end{array}\right.$;
(2)解不等式①,得:x≥1,
解不等式②,得:x<3,
∴不等式组的解集为1≤x<3,
则不等式组的整数解为1、2.
点评 本题考查的是换元法解二元一次方程组和解一元一次不等式组,熟练掌握换元法解方程组和解不等式组的基本步骤是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,M、N分别是边AB、AC的中点,D是边BC延长线上的一点,且CD=$\frac{1}{2}$BC,联结CM、DN.
已知:如图,在△ABC中,M、N分别是边AB、AC的中点,D是边BC延长线上的一点,且CD=$\frac{1}{2}$BC,联结CM、DN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
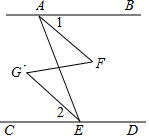 如图,已知∠BAE+∠AED=180°,∠1=∠2,那么∠F=∠G,为什么?
如图,已知∠BAE+∠AED=180°,∠1=∠2,那么∠F=∠G,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
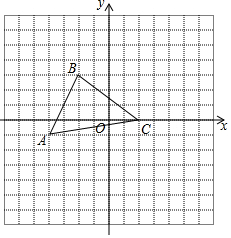 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-4,-1)、B(-2,3)、C(2,0),将△ABC先向右平移5个单位,再向上平移3个单位,得到△A1B1C1.
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-4,-1)、B(-2,3)、C(2,0),将△ABC先向右平移5个单位,再向上平移3个单位,得到△A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com