练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    求证：菱形四条边的中点在以对角线的交点为圆心的同一圆上．

    答案：
    解析：

    　　已知：如下图所示，菱形ABCD的对角线AC和BD相交于点O，E，F，G，H分别是AB，BC，CD，AD的中点．

    　　求证：E，F，G，H四个点在以O为圆心的同一圆上．

    　　证明：连接OE，OF，OG，OH，

    　　∵四边形ABCD为菱形，

    　　∴AB＝BC＝CD＝AD，∴AC⊥BD，

    　　又∵E，F，G，H分别为AB，BC，CD，AD的中点，

    　　∴OE＝OF＝OG＝OH＝AB，

    　　∴E，F，G，H四点在以O为圆心的同一圆上．

    　　分析：若E，F，G，H四个点在同一个圆上，根据圆的概念，它们应到定点的距离都等于定长，因为E，F，G，H是菱形各边的中点，根据菱形的对角线互相垂直，以及直角三角形斜边上的中线等于斜边的一半，得到E，F，G，H到O点的距离都等于菱形边长的一半，此题得证．

    　　小结：证明点共圆，只需证明这些点到定点的距离相等即可．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在探究矩形的性质时，小明得到了一个有趣的结论：矩形两条对角线的平方和等于四条边的平方和．如图1，在矩形ABCD中，由勾股定理，得AC2=AB2+BC2，BD2=AB2+AD2，又CD=AB，AD=BC，所以AC2+BD2=AB2+BC2+CD2+AD2=2（AB2+BC2）．
    小亮对菱形进行了探究，也得到了同样的结论，于是小亮猜想：任意平行四边形两条对角线的平方和等于四条边的平方和．请你解决下列问题：
    （1）如图2，已知：四边形ABCD是菱形，求证：AC2+BD2=2（AB2+BC2）；
    （2）你认为小亮的猜想是否成立，如果成立，请利用图3给出证明；如果不成立，请举反例说明；
    （3）如图4，在△ABC中，BC、AC、AB的长分别为a、b、c，AD是BC边上的中线．试求AD的长．（结果用a，b，c表示）
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    （2013•鼓楼区一模）问题提出：
    规定：四条边对应相等，四个角对应相等的两个四边形全等．
    我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究．
    初步思考：
    在两个四边形中，我们把“一条边对应相等”或“一个角对应相等”称为一个条件．满足4个条件的两个四边形不一定全等，如边长相等的正方形与菱形就不一定全等．类似地，我们容易知道两个四边形全等至少需要5个条件．
    深入探究：
    小莉所在学习小组进行了研究，她们认为5个条件可分为以下四种类型：
    Ⅰ一条边和四个角对应相等；Ⅱ二条边和三个角对应相等；
    Ⅲ三条边和二个角对应相等；Ⅳ四条边和一个角对应相等．
    （1）小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等，请你举例说明．
    （2）小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等，请你结合下图进行证明．
    已知：如图，
    四边形ABCD和四边形A1B1C1D1中，AB=A1B1，BC=B1C1，CD=C1D1，DA=D1A1，∠B=∠B1．
    四边形ABCD和四边形A1B1C1D1中，AB=A1B1，BC=B1C1，CD=C1D1，DA=D1A1，∠B=∠B1．
    ．
    求证：
    四边形ABCD≌四边形A1B1C1D1
    四边形ABCD≌四边形A1B1C1D1
    ．
    证明：

    （3）小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类，他以四边形ABCD和四边形A1B1C1D1为例，分为以下几类：
    ①AB=A1B1，AD=A1D1，∠A=∠A1，∠B=∠B1，∠C=∠C1；
    ②AB=A1B1，AD=A1D1，∠A=∠A1，∠B=∠B1，∠D=∠D1；
    ③AB=A1B1，AD=A1D1，∠B=∠B1，∠C=∠C1，∠D=∠D1；
    ④AB=A1B1，CD=C1D1，∠A=∠A1，∠B=∠B1，∠C=∠C1．
    其中能判定四边形ABCD和四边形A1B1C1D1全等的是
    ①②③
    ①②③
    （填序号），概括可得“全等四边形的判定方法”，这个判定方法是
    有一组邻边和三个角对应相等的两个四边形全等
    有一组邻边和三个角对应相等的两个四边形全等
    ．
    （4）小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类，请你仿照小刚的方法先进行分类，再概括得出一个全等四边形的判定方法．

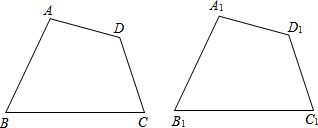
    查看答案和解析>>

    科目：初中数学 来源： 题型：

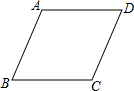    我们知道，小学对菱形的认识是：四条边都相等的四边形．到了初中，对菱形的定义是：有一组邻边相等的平行四边形，请你利用初中的定义来说明小学认识的合理性．先补全题目，再完成证明：
    如图，在?ABCD中，已知
    AB=AD
    AB=AD
    ，
    求证：
    四边形ABCD是菱形
    四边形ABCD是菱形
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在探究矩形的性质时，小明得到了一个有趣的结论：矩形两条对角线的平方和等于四条边的平方和．如图1，在矩形ABCD中，由勾股定理，得AC2=AB2+BC2，BD2=AB2+AD2，又CD=AB，AD=BC，所以AC2+BD2=AB2+BC2+CD2+AD2=2（AB2+BC2）．
    小亮对菱形进行了探究，也得到了同样的结论，于是小亮猜想：任意平行四边形两条对角线的平方和等于四条边的平方和．请你解决下列问题：
    （1）如图2，已知：四边形ABCD是菱形，求证：AC2+BD2=2（AB2+BC2）；
    （2）你认为小亮的猜想是否成立，如果成立，请利用图3给出证明；如果不成立，请举反例说明；
    （3）如图4，在△ABC中，BC、AC、AB的长分别为a、b、c，AD是BC边上的中线．试求AD的长．（结果用a，b，c表示）

    查看答案和解析>>

    科目：初中数学 来源：2011年安徽省马鞍山市成功学校中考数学一模试卷（解析版） 题型：解答题

    在探究矩形的性质时，小明得到了一个有趣的结论：矩形两条对角线的平方和等于四条边的平方和．如图1，在矩形ABCD中，由勾股定理，得AC2=AB2+BC2，BD2=AB2+AD2，又CD=AB，AD=BC，所以AC2+BD2=AB2+BC2+CD2+AD2=2（AB2+BC2）．
    小亮对菱形进行了探究，也得到了同样的结论，于是小亮猜想：任意平行四边形两条对角线的平方和等于四条边的平方和．请你解决下列问题：
    （1）如图2，已知：四边形ABCD是菱形，求证：AC2+BD2=2（AB2+BC2）；
    （2）你认为小亮的猜想是否成立，如果成立，请利用图3给出证明；如果不成立，请举反例说明；
    （3）如图4，在△ABC中，BC、AC、AB的长分别为a、b、c，AD是BC边上的中线．试求AD的长．（结果用a，b，c表示）

    查看答案和解析>>

    同步练习册答案