
【题目】在平面直角坐标系xOy中,点P的坐标为(![]() ,
,![]() ),点Q的坐标为(
),点Q的坐标为(![]() ,
,![]() ),且
),且![]() ,
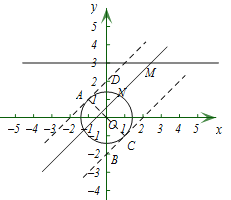
,![]() ,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
(1)已知点A的坐标为(1,0).
①若点B的坐标为(3,1)求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为![]() ,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.

【答案】(1)①2;②![]() 或
或 ![]() ;(2)1≤m≤5 或者
;(2)1≤m≤5 或者![]() .
.
【解析】
试题分析:(1)①由相关矩形的定义可知:要求A与B的相关矩形面积,则AB必为对角线,利用A、B两点的坐标即可求出该矩形的底与高的长度,进而可求出该矩形的面积;
②由定义可知,AC必为正方形的对角线,所以AC与x轴的夹角必为45,设直线AC的解析式为;y=kx+b,由此可知k=±1,再(1,0)代入y=kx+b,即可求出b的值;
(2)由定义可知,MN必为相关矩形的对角线,若该相关矩形的为正方形,即直线MN与x轴的夹角为45°,由因为点N在圆O上,所以该直线MN与圆O一定要有交点,由此可以求出m的范围.
试题解析:(1)①∵A(1,0),B(3,1),由定义可知:点A,B的“相关矩形”的底与高分别为2和1,∴点A,B的“相关矩形”的面积为2×1=2;
②由定义可知:AC是点A,C的“相关矩形”的对角线,又∵点A,C的“相关矩形”为正方形,∴直线AC与x轴的夹角为45°,设直线AC的解析为:y=x+m或y=﹣x+n,把(1,0)分别y=x+m,∴m=﹣1,∴直线AC的解析为:y=x﹣1,把(1,0)代入y=﹣x+n,∴n=1,∴y=﹣x+1,综上所述,若点A,C的“相关矩形”为正方形,直线AC的表达式为y=x﹣1或y=﹣x+1;
(2)设直线MN的解析式为y=kx+b,∵点M,N的“相关矩形”为正方形,∴由定义可知:直线MN与x轴的夹角为45°,∴k=±1,∵点N在⊙O上,∴当直线MN与⊙O有交点时,点M,N的“相关矩形”为正方形,当k=1时,作⊙O的切线AD和BC,且与直线MN平行,其中A、C为⊙O的切点,直线AD与y轴交于点D,直线BC与y轴交于点B,连接OA,OC,把M(m,3)代入y=x+b,∴b=3﹣m,∴直线MN的解析式为:y=x+3﹣m.∵∠ADO=45°,∠OAD=90°,∴OD=![]() OA=2,∴D(0,2);
OA=2,∴D(0,2);
同理可得:B(0,﹣2),∴令x=0代入y=x+3﹣m,∴y=3﹣m,∴﹣2≤3﹣m≤2,∴1≤m≤5,当k=﹣1时,把M(m,3)代入y=﹣x+b,∴b=3+m,∴直线MN的解析式为:y=x+3+m,同理可得:﹣2≤3+m≤2,∴﹣5≤m≤﹣1;
综上所述,当点M,N的“相关矩形”为正方形时,m的取值范围是:1≤m≤5或﹣5≤m≤﹣1.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】八(3)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图2,先过B点作AB的垂线,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读回答下列问题:
(1)方案(Ⅰ)是否可行?请说明理由.
(2)方案(Ⅱ)是否可行?请说明理由.
(3)方案(Ⅲ)中作BF⊥AB,ED⊥BF的目的是;若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立? .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC.∠EBC=∠E=60°,若BE=6,DE=2,则BC的长度是( ) 
A.6
B.8
C.9
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一副三角尺的两个直角顶点O重合在一起,在同一平面内旋转其中一个三角尺.
(1)如图1,若 ∠ B O C = 70° ,则 ∠ A O D = 度 .
(2)如图2,若 ∠ B O C = 50°,则 ∠ A O D = 度 .
(3)如图1,请猜想 ![]() 与
与 ![]() 的关系,并写出理由.
的关系,并写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:关于三角函数还有如下的公式:
sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)=![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan75°=tan(45°+30°)=![]() =
=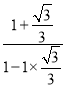 =
=![]()
根据以上阅读材料,请选择适当的公式解答下面问题:
(1)计算:sin15°;
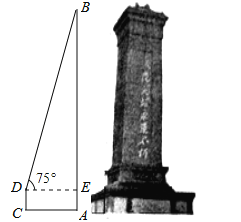
(2)某校在开展爱国主义教育活动中,来到烈士纪念碑前缅怀和纪念为国捐躯的红军战士.李三同学想用所学知识来测量如图纪念碑的高度.已知李三站在离纪念碑底7米的C处,在D点测得纪念碑碑顶的仰角为75°,DC为![]() 米,请你帮助李三求出纪念碑的高度.
米,请你帮助李三求出纪念碑的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不能判断四边形ABCD是平行四边形的是( )
A. AB=CD,AD=BC B. AB∥CD,AD=BC
C. AB∥CD,AD∥BC D. ∠A=∠C,∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. ﹣2x2﹣3x2=﹣5x2 B. 6x2y3+2xy2=3xy
C. 2x33x2=6x6 D. (a+b)2=a2﹣2ab+b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把函数y=x的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数y=2x的图象;也可以把函数y=x的图象上各点的横坐标变为原来的![]() 倍,纵坐标不变,得到函数y=2x的图象.
倍,纵坐标不变,得到函数y=2x的图象.
类似地,我们可以认识其他函数.
(1)把函数![]() 的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数
的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数![]() 的图象;也可以把函数
的图象;也可以把函数![]() 的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数
的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数![]() 的图象.
的图象.
(2)已知下列变化:①向下平移2个单位长度;②向右平移1个单位长度;③向右平移![]() 个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的
个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的![]() 倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.
倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.
(Ⅰ)函数![]() 的图象上所有的点经过④→②→①,得到函数 的图象;
的图象上所有的点经过④→②→①,得到函数 的图象;
(Ⅱ)为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象上所有的点 .
的图象上所有的点 .
A.①→⑤→③B.①→⑥→③C.①→②→⑥D.①→③→⑥
(3)函数![]() 的图象可以经过怎样的变化得到函数
的图象可以经过怎样的变化得到函数![]() 的图象?(写出一种即可)
的图象?(写出一种即可)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com