
【题目】如图,O是直线AB上的一点,∠AOC=45°,OE是∠BOC内部的一条射线,且OF平分∠AOE.
(1)如图1,若∠COF=35°,求∠EOB的度数;
(2)如图2,若∠EOB=40°,求∠COF的度数;
(3)如图3,∠COF与∠EOB有怎样的数量关系?请说明理由.

【答案】(1)∠EOB=20°;(2)∠COF= 25°;(3)∠EOB+2∠COF=90°,理由见解析.
【解析】
(1)OF平分∠AOE得出∠AOF=∠EOF,再利用∠BOE与∠AOE是邻补角这一关系解答即可;
(2)分析方法如上题,OF平分∠AOE得出∠AOF=∠EOF,再利用∠BOE与∠AOE是邻补角相加等于180°解答即可;
(3)分析方法同上,设∠COF与∠EOB的度数分别是α和β,再计算得出数量关系即可.
(1)∵∠AOC=45°,∠COF=35°
∴∠AOF=∠AOC+∠COF=80°
∵OF平分∠AOE,
∴∠AOE=2∠AOF=160°
∵∠AOB是平角
∴∠AOB=180°
∴∠EOB=∠AOB﹣∠AOE=20°
答:∠EOB的度数是20°.
(2)∠AOE=180°﹣40°=140°
∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=70°
∠AOE=70°
∴∠COF=∠AOF﹣∠AOC=70°﹣45°=25°
答:∠COF的度数是25°.
(3)∠EOB+2∠COF=90°,理由如下:
设∠COF=α,∠BOE=β
∵∠AOB是平角,
∴∠AOE=180°﹣β
∵OF平分∠AOE,
∴2∠AOF=∠AOE=180°﹣β
∴2α=2∠COF=2(∠AOF﹣∠AOC )
=2∠AOF﹣2∠AOC
=180°﹣β﹣2×45°=90°﹣β
∴2α+β=90°
即∠EOB+2∠COF=90°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为点A,射线BM⊥AB,垂足为点B,AB=12cm,AC=6cm.动点E从A点出发以3cm/s沿射线AN运动,动点D在射线BM上,随着E点运动而运动,始终保持ED=CB.当点E经过______s时,△DEB与△BCA全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: ![]() ,
,![]() .
.
(1)当x=1和-1时,分别求P,Q的值;
(2)当x=19时,P的值为a, Q的值为b,当x=-19时,分别求P, Q的值(用含a,b的代数式表示);
(3)当x=m时,P, Q的值分别为c, d; 当x=-m时,P, Q的值分别为e, f,则在c,d, e, f四个有理数中,以下判断正确的是 (只要填序号即可).
①有两个相等的正数;②有两个互为相反数;③至多有两个正数;④至少有两个正数;⑤至多有一个负数;⑥至少有一个负数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B在数轴上对应的数分别用a,b表示,并且关于x的多项式(a+10)x7+2xb-15﹣4是五次二项式,P,Q是数轴上的两个动点.
(1)a=_____,b=_____;
(2)设点P在数轴上对应的数为x,PA+PB=40,求x的值;
(3)动点P,Q分别从A,B两点同时出发向左运动,点P,Q的运动速度分别为3个单位长度/秒和2个单位长度/秒.点M是线段PQ中点,设运动的时间小于6秒,问6AM+5PB的值是否发生变化?若不变,求其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
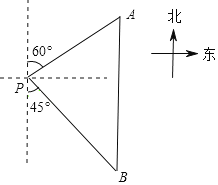
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠B=∠D.点EF分别在AB、CD上.连接AC,分别交DE、BF于G、H.求证:∠1+∠2=180°

证明:∵AB∥CD,
∴∠B=_____._____
又∵∠B=∠D,
∴_____=_____.(等量代换)
∴_____∥_____._____
∴∠l+∠2=180°._____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com