Question

10．如图，A点在半径为2的⊙O上，过线段OA上的一点P作直线m，与⊙O过A点的切线交于点B，且∠APB=60°，设OP=x，则△PAB的面积y关于x的函数图象大致是（　　）

• A．
• B．
• C．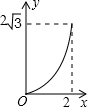
• D．

Answer 1

分析 根据已知得出S与x之间的函数关系式，进而得出函数是二次函数，当x=-$\frac{b}{2a}$=2时，S取到最小值为：$\frac{4ac-{b}^{2}}{4a}$=0，即可得出图象．

解答 解：∵A点在半径为2的⊙O上，过线段OA上的一点P作直线m，与⊙O过A点的切线交于点B，且∠APB=60°，
∴AO=2，OP=x，则AP=2-x，
∴tan60°=$\frac{AB}{PA}$=$\sqrt{3}$，
解得：AB=$\sqrt{3}$（2-x）=-$\sqrt{3}$x+2$\sqrt{3}$，
∴S_△ABP=$\frac{1}{2}$×PA×AB=$\frac{1}{2}$（2-x）•$\sqrt{3}$•（-x+2）=$\frac{\sqrt{3}}{2}$x²-2$\sqrt{3}$x+2$\sqrt{3}$，
故此函数为二次函数，
∵a=$\frac{\sqrt{3}}{2}$＞0，
∴当x=-$\frac{b}{2a}$=2时，S取到最小值为：$\frac{4ac-{b}^{2}}{4a}$=0，
根据图象得出只有D符合要求．
故选：D．

点评 此题主要考查了动点函数的图象，根据已知得出S与x之间的函数解析式是解题关键．