
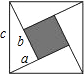
 如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么?
如图,由4个边长为a,b,c的直角三角形拼成一个正方形,中间有一个小正方形的开口(图中阴影部分),试用不同的方法计算这个阴影部分的面积,你发现了什么?| 1 |
| 2 |


科目:初中数学 来源: 题型:
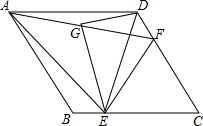 如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF.
如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,∠DAE=∠BAF. 查看答案和解析>>
科目:初中数学 来源: 题型:
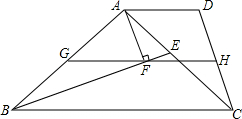 如图,在梯形ABCD中,AD∥BC,BE是△ABC的角平分线,AF⊥BE于F,过F作GH∥BC分别交AB,CD于G,H.求证:
如图,在梯形ABCD中,AD∥BC,BE是△ABC的角平分线,AF⊥BE于F,过F作GH∥BC分别交AB,CD于G,H.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 时间(天) | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量(件) | 94 | 90 | 84 | 76 | 24 | … |
| 1 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
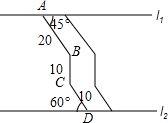 如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.
如图,两条平行景观长廊l1和l2之间有一条折线通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m.查看答案和解析>>
科目:初中数学 来源: 题型:
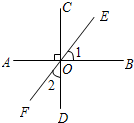 如图3,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(
如图3,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是(| A、∠1=∠2 |
| B、∠1+∠2=90° |
| C、∠1+∠2=180° |
| D、无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com