
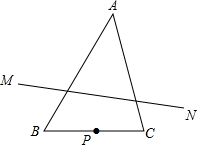
 如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$.
如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$. 分析 连接AM、AN、AP,过点A作AD⊥MN于点D,由对称性可知AM=AP=AN、△MAN等腰直角三角形,进而即可得出MN=$\sqrt{2}$AP,再根据AP的取值范围即可得出线段MN长的取值范围.
解答 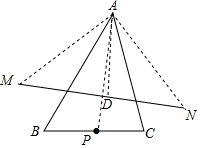 解:连接AM、AN、AP,过点A作AD⊥MN于点D,如图所示.
解:连接AM、AN、AP,过点A作AD⊥MN于点D,如图所示.
∵点P关于直线AB,AC的对称点分别为M,N,
∴AM=AP=AN,∠MAB=∠PAB,∠NAC=∠PAC,
∴△MAN等腰直角三角形,
∴∠AMD=45°,
∴AD=MD=$\frac{\sqrt{2}}{2}$AM,MN=$\sqrt{2}$AM.
∵AB=4,∠B=60°,
∴2$\sqrt{3}$≤AP≤4,
∵AM=AP,
∴2$\sqrt{6}$≤MN≤4$\sqrt{2}$.
故答案为:2$\sqrt{6}$≤MN<4$\sqrt{2}$.
点评 本题考查了轴对称的性质,等腰直角三角形的判定和性质,解题的关键是证得△AMN是等腰直角三角形.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
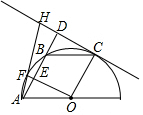 如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
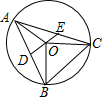 如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )
如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
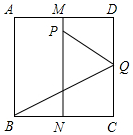 如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于$\frac{1}{3}$.
如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )
如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )| A. | (2n-1,2n-1) | B. | (2n-1+1,2n-1) | C. | (2n-1,2n-1) | D. | (2n-1,n) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
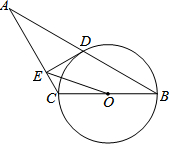 如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE是⊙O的切线,连结OD,OE
如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE是⊙O的切线,连结OD,OE查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com