
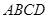 中,对角线
中,对角线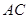 平分
平分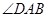 .
.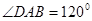 ,
,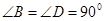 时,求证:
时,求证: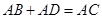 ;
;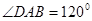 ,
,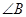 与
与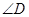 互补时,线段
互补时,线段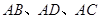 有怎样的数量关系?写出你的猜想,并给予证明;
有怎样的数量关系?写出你的猜想,并给予证明;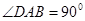 ,
,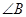 与
与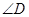 互补时,线段
互补时,线段 有怎样的数量关系?直接写出你的猜想.
有怎样的数量关系?直接写出你的猜想.
 中,由
中,由 平分
平分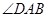 ,
,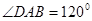
 ,又
,又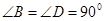 ,
,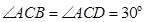 ,
,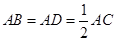 ,即可得到结论;
,即可得到结论;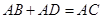 ;
;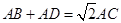
 中,由
中,由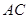 平分
平分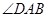 ,
,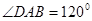 可得
可得 ,又
,又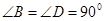 ,可得
,可得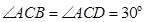 ,根据含30°角的直角三角形的性质可得
,根据含30°角的直角三角形的性质可得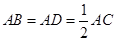 ,即可得到结论;
,即可得到结论; 点分别作CE⊥
点分别作CE⊥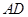 于E,CF⊥
于E,CF⊥ 交AB延长线于F,根据角平分线的性质可得CE=CF,由
交AB延长线于F,根据角平分线的性质可得CE=CF,由  ,
, 可得
可得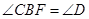 ,再结合
,再结合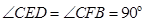 可证得
可证得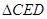 ≌
≌ ,即得
,即得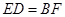 ,再结合(1)中
,再结合(1)中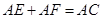 即可求得结果;
即可求得结果; 中,
中,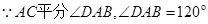 ,
, .
. ,
,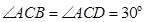 .
.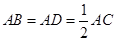 .
.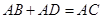 ;
;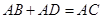 .
. 点分别作CE⊥
点分别作CE⊥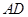 于E,CF⊥
于E,CF⊥ 交AB延长线于F,
交AB延长线于F,

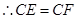
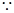
 ,
,
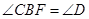
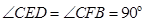
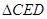 ≌
≌
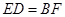
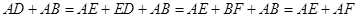 .
.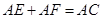 .
.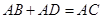 ;
;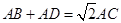 .
.

科目:初中数学 来源:不详 题型:填空题
 ≤r<2时,S的取值范围是 .
≤r<2时,S的取值范围是 .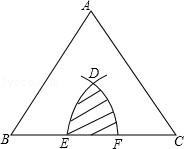
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 是等边三角形,D是射线BC上的一个动点(与点B、C不重合),
是等边三角形,D是射线BC上的一个动点(与点B、C不重合), 是以AD为边的等边三角形,过点E作
是以AD为边的等边三角形,过点E作 ,交射线AC于点F,连结BE.
,交射线AC于点F,连结BE. ,当点D在线段BC上运动时。①求证:
,当点D在线段BC上运动时。①求证: ;②探究四边形BCFE是怎样的四边形?并说明理由;
;②探究四边形BCFE是怎样的四边形?并说明理由;
 ,当点D在线段BC的延长线上运动时,请直接写出(1)的两个结论是否依然成立;
,当点D在线段BC的延长线上运动时,请直接写出(1)的两个结论是否依然成立;
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
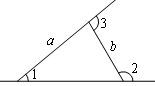
| A.38° | B.40° | C.42° | D.45° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
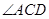 的平分线交BA延长线于点E,
的平分线交BA延长线于点E,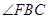 的平分线交AC延长线于点G.若CE =" BC" = BG,则
的平分线交AC延长线于点G.若CE =" BC" = BG,则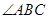 的度数 度.
的度数 度.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
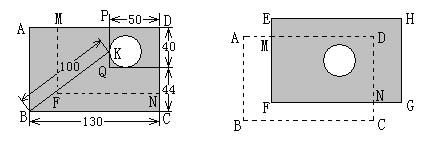
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com