
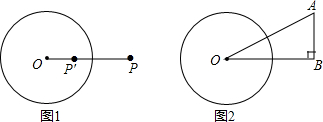
分析 先证明△AOB∽△B′OA′,然后根据相似三角形的对应角相等可以推知∠OA′B′=∠OBA=90°,根据勾股定理即可求得.
解答 解:∵A′、B′分别是点A、B关于圆O的反演点,
∴$\frac{OA}{OB′}$=$\frac{OB}{OA′}$,
又∵∠O=∠O,
∴△AOB∽△B′OA′,
∴∠OA′B′=∠OBA=90°,
∵AB=2,BO=4,圆O的半径为2,
∴OA=2$\sqrt{5}$,
∴OA′=$\frac{{r}^{2}}{OA}$=$\frac{2\sqrt{5}}{5}$,OB′=$\frac{{r}^{2}}{OB}$=1,
∴A′B′=$\sqrt{{OB′}^{2}{-OA′}^{2}}$=$\frac{\sqrt{5}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查了圆的综合题.解题时涉及到的知识点有:相似三角形的判定与性质、圆周角定理、等式的性质等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又散步走回家,图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )
如图图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又散步走回家,图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )| A. | 体育场离张强家2.5km | |
| B. | 张强从家到体育场用了15min | |
| C. | 张强在体育场锻炼了15min | |
| D. | 张强散步回家的平均速度是2.5km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
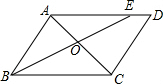 如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )
如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )| A. | 9cm | B. | 7cm | C. | 6cm | D. | 8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学综合实践小组同学,想测量金龙山观音大佛的高度,他们在山脚下的D处测得山顶B的仰角为30°,沿着山脚向前走了4米达到E处,测得观音大佛的头顶A的倾角为45°,已知金龙山的山顶距地面的标高(线段BC的长度)为60米,请计算观音大佛的高度为多少米?(结果精确到0.1米,$\sqrt{3}$≈1.73)
某中学综合实践小组同学,想测量金龙山观音大佛的高度,他们在山脚下的D处测得山顶B的仰角为30°,沿着山脚向前走了4米达到E处,测得观音大佛的头顶A的倾角为45°,已知金龙山的山顶距地面的标高(线段BC的长度)为60米,请计算观音大佛的高度为多少米?(结果精确到0.1米,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
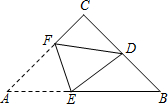 如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为$\frac{3}{5}$.
如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为$\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com