
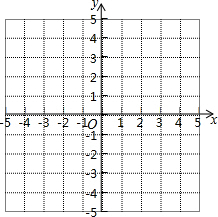
 已知:一次函数y=2x+4
已知:一次函数y=2x+4科目:初中数学 来源: 题型:解答题
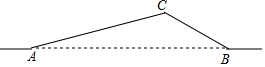 如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 本次抽样测试的学生人数是40 | |
| B. | 在图1中,∠α的度数是126° | |
| C. | 该校九年级有学生500名,估计D级的人数为80 | |
| D. | 从被测学生中随机抽取一位,则这位学生的成绩是A级的概率为0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
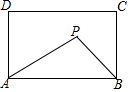 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )| A. | $\sqrt{29}$ | B. | $\sqrt{34}$ | C. | 5$\sqrt{2}$ | D. | $\sqrt{41}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
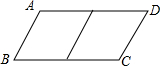 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
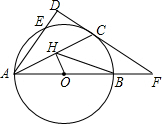 如图,AB是⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于E,DE=2,CD=4.
如图,AB是⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于E,DE=2,CD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com