Question

15．如图，Rt△ABC的三个顶点分别是A（-3，2），B（0，4），C（0，2），结合所给的平面直角坐标系解答下列问题：
（1）画出△ABC以点C为旋转中心旋转180°后对应的△A₁B₁C；
（2）平移△ABC，若点A的对应点A₂的坐标为（0，-4），画出平移后对应的△A₂B₂C₂；
（3）若将△A₁B₁C绕某一点旋转可以得到△A₂B₂C₂，请直接写出旋转中心的坐标．

Answer 1

分析 （1）延长AC至A₁，使AC=A₁C，因为BC=OC，所以点B₁与点O重合，则将A₁、O、C连接成三角形即可；
（2）由A（-3，2）与对应点A₂的坐标为（0，-4），可知向下平移6个单位，再向右平移3个单位，依次取出点B₂、C₂即可；
（3）对应点连线的交点既是旋转中心E，写出坐标．

解答 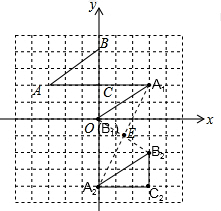解：（1）延长AC至A₁，点B₁与点O重合，连接A₁C、B₁C、A₁B₁，则△A₁CB₁就是所求三角形；
（2）取B₂（3，-2），C₂（4，-3），连成△A₂B₂C₂；
（3）连接A₁A₂、B₁B₂，交于点E，则点E就是旋转中心，E（1.5，-1）．

点评 本题是作图题，考查了旋转变换和平移变换；作旋转变换图形的具体作法是：若旋转180°时，利用在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形；作平移变换图形的具体作法是：作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．