
【题目】元旦期间,某超市对出售![]() 、
、![]() 两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
两种商品开展元旦促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
商品 |
|
| |
标价(单位:元) |
|
| |
方案一 | 每件商品出售价格 | 按标价降价 | 按标价降价 |
方案二 | 若所购商品超过 | ||
(1)某单位购买![]() 商品
商品![]() 件,
件,![]() 商品
商品![]() 件,共花费
件,共花费![]() 元,试求
元,试求![]() 的值;
的值;
(2)在(1)求出的![]() 值的条件下,若某单位购买
值的条件下,若某单位购买![]() 商品
商品![]() 件(
件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数比
商品的件数比![]() 商品件数的
商品件数的![]() 倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
倍还多一件,请问该单位选择哪种方案才能获得最大优惠?请说明理由.
【答案】(1)15;(2)当x≤33时,选择方案一优惠最大;当x>33时,选择方案二优惠更大,理由见解析
【解析】
(1)根据题意列出40×200×0.8+30×300×(1-a%)=14050方程解答即可;
(2)根据题意列出两种方案,进而比较即可.
(1)由题意有,40×200×0.8+30×300×(1-a%)=14050
整理得:(1-a%)=0.85,
所以a=15;
(2)根据题意得:x+2x+1=100得:x=33当总数不足101时,即选择方案一得最大优惠;
当总数达到或超过101,即x>33时,
方案一需付款:200×0.8x+300×0.85(2x+1)=160x+510x+255=670x+255
方案二需付款:[200x+300(2x+1)]×0.82=656x+246,
∵(670x+255)-(656x+246)=14x+9>0
∴选方案二优惠更大
综上所述:当x≤33时,选择方案一优惠最大;当x>33时,选择方案二优惠更大.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交两轴于点
分别交两轴于点![]() ,点
,点![]() 的横坐标为4,点
的横坐标为4,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)在平面内是否存在这样的点![]() ,使以
,使以![]() 为顶点的四边形为平行四边形?若存在,请求出点
为顶点的四边形为平行四边形?若存在,请求出点![]() 的坐标;若不存在,不必说明理由.
的坐标;若不存在,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.
(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当k=![]() 时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
①求CD的长;
②设△COD的OC边上的高为h,当t为何值时,h的值最大?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根.
(1)是否存在实数k,使(2x1-x2)(x1-2x2)=-![]() 成立?若存在,求出k的值;若不存在,请说明理由;
成立?若存在,求出k的值;若不存在,请说明理由;
(2)求使![]() -2的值为整数的整数k的值.
-2的值为整数的整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:
当温度达到设定温度﹣20℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到﹣4℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至一20℃时,制冷再次停止,..
按照以上方式循环进行
同学们记录了44min 内15个时间点冷柜中的温度y(℃) 随时间x(min) 的变化情况,制成下表:
时间x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
温度y/℃ | … | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | ﹣8 | ﹣12 | ﹣16 | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | a | ﹣20 | … |
(1)通过分析发现,冷柜中的温度y是时间x的函数.
①当4≤x<20时,写出一个符合表中数据的函数解析式 ;
②当20≤x<24时,写出一个符合表中数据的函数解析式 ;
(2)温度不低于﹣8℃的持续时间为 min;
(3)A的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A、C表示的数为﹣14、4,甲、乙两点分别从A、C两点出发,同时相向而行,已知甲的速度为4个单位/秒,乙的速度为3个单位/秒.
![]()
(1)求相遇点表示的数;
(2)数轴上有一点B表示的数为﹣4,甲到达点C后调头返回,求运动多少秒后,甲、乙两点到B点的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
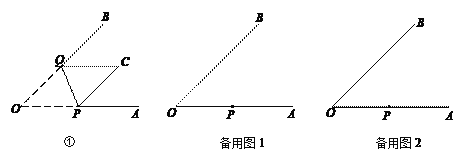
【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2 cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处.
(1)①当PC∥QB时,OQ= cm;
②在OB上找一点Q,使PC⊥QB(尺规作图,保留作图痕迹);
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com