
【题目】如图,在平行四边形ABCD中,EF∥AB,DE:AE=2:3,△BDC的面积为25,则四边形AEFB的面积为( )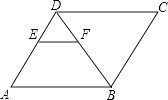
A.25
B.9
C.21
D.16
科目:初中数学 来源: 题型:
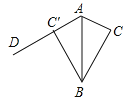
【题目】如图,△ABC的面积为6,AC3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的![]() 处,P为直线AD上的任意一点,则线段BP的最短长度为_____________.
处,P为直线AD上的任意一点,则线段BP的最短长度为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.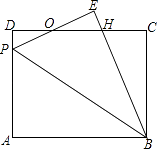
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(x﹣1)2+k分别与x轴、y轴交于A、B、C三点,点A在点B的左侧,直线y=﹣ ![]() x+2经过点B,且与y轴交于点D.
x+2经过点B,且与y轴交于点D.
(1)如图1,求k的值;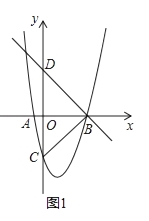
(2)如图2,在第一象限的抛物线上有一动点P,连接AP,过P作PE⊥x轴于点E,过E作EF⊥AP于点F,过点D作平行于x轴的直线分别与直线FE、PE交于点G、H,设点P的横坐标为t,线段GH的长为d,求d与t的函数关系式,并直接写出t的取值范围;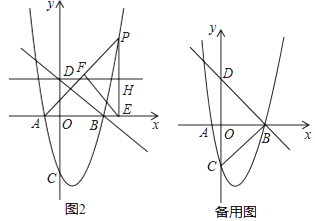
(3)在(2)的条件下,过点G作平行于y轴的直线分别交AP、x轴和抛物线于点M、T和N,tan∠MEA= ![]() ,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )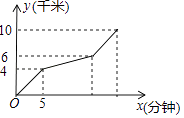
A.15分钟
B.20分钟
C.25分钟
D.30分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A.6
B.13
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
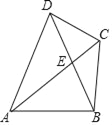
【题目】如图,在四边形ABCD中,AB⊥BC,对角线AC、BD相交于点E,E为BD中点,且AD=BD,AB=2,∠BAC=30°,则DC=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com