
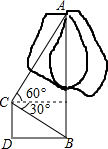
 为改变哈尔滨市的交通状况,在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°,那么距离B点7米远,才是安全区域.(结果保留整数,$\sqrt{3}$≈1.732)
为改变哈尔滨市的交通状况,在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°,那么距离B点7米远,才是安全区域.(结果保留整数,$\sqrt{3}$≈1.732) 分析 根据题意可知所求的问题实际上就是求AB得长,由题目中的数据和锐角三角函数可以求得AB的长,从而本题得以解决.
解答  解:由题意可得,如右图所示,
解:由题意可得,如右图所示,
BD=3米,∠CDB=90°,
∵CE∥DB,∠ECB=30°,
∴∠ECB=∠CBD=30°,
∴CD=BD•tan∠CBD=3×tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}米$,
∵CE=BD=3米,∠CEA=90°,∠ACE=60°,
∴AE=CE•tan60°=3×$\sqrt{3}$=3$\sqrt{3}$米,
∴AB=AE+EB=$\sqrt{3}+3\sqrt{3}$=4$\sqrt{3}$≈4×1.732=6.928≈7米,
故答案为:7.
点评 本题考查解直角三角形的应用-仰角俯角问题,解答此类问题的关键是明确题意,利用锐角三角函数解答,注意最后结果要保留整数.


科目:初中数学 来源: 题型:解答题
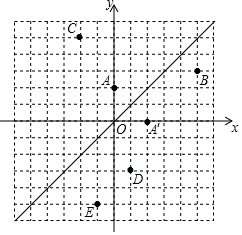 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 周长相等的两个三角形全等 | |
| B. | 等底等高的两个三角形全等 | |
| C. | 有两边和一角对应相等的两个三角形全等 | |
| D. | 有一条直角边和斜边上的高对应相等的两个直角三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若$\frac{AD}{BD}=\frac{3}{4}$,DE=4,则BC的长为$\frac{28}{3}$.
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若$\frac{AD}{BD}=\frac{3}{4}$,DE=4,则BC的长为$\frac{28}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
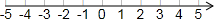 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y>1 | B. | 0<y<1 | C. | y>2 | D. | 0<y<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com