
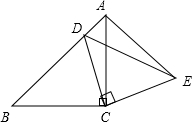
 已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,试说明:
已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,试说明:分析 (1)根据SAS即可证明.
(2)欲证明AD2+AE2=DE2,只要证明∠DAE=90°即可.
解答 证明:(1)∵△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,
∴BC=CA,CD=CE,∠BCD=ECA,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD.
(2)∵BC=AC,
∴∠ACB=90°,
∴∠B=∠CAB=45°
∵△ACE≌△BCD,
∴∠CAE=∠CBD=45°,
∴∠DAE=∠CAB+∠CAE=90°,
∴AD2+AE2=ED2.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,正确寻找全等三角形,属于基础题,中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对普宁市辖区水质情况的调查 | |
| B. | 对普宁电视台“商城聚焦”栏目收视率的调查 | |
| C. | 对某小区每天丢弃塑料袋数量的调查 | |
| D. | 对乘坐飞机的旅客是否违规携带违禁物品的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q,则结论:①AE=CD;②CQ=CA;③PQ∥AD;④EP=QD中,其中正确结论是①③④.
如图,已知B是线段AD上的一点,△ABC、△BDE均为等边三角形,AE交BC于P,CD交BE于Q,则结论:①AE=CD;②CQ=CA;③PQ∥AD;④EP=QD中,其中正确结论是①③④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com