
 如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )
如图,∠ABC>∠ADC,且∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间存在的等量关系是( )| A. | ∠AEC=∠ABC-2∠ADC | B. | ∠AEC=$\frac{∠ABC-∠ADC}{2}$ | ||
| C. | ∠AEC=$\frac{1}{2}$∠ABC-∠ADC | D. | ∠AEC=$\frac{∠ABC-∠ADC}{3}$ |
分析 首先延长BC交AD于点F,由三角形外角的性质,可得∠BCD=∠B+∠BAD+∠D,又由角平分线的性质,即可求得答案.
解答 解:如图,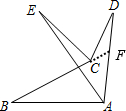
延长BC交AD于点F,
∵∠BFD=∠B+∠BAD,
∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D,
∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=$\frac{1}{2}$∠BCD,∠EAD=∠EAB=$\frac{1}{2}$∠BAD,
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB-∠ECB=∠B+∠BAE-$\frac{1}{2}$∠BCD=∠B+∠BAE-$\frac{1}{2}$(∠B+∠BAD+∠D)=$\frac{1}{2}$(∠B-∠D),
即∠AEC=$\frac{∠ABC-∠ADC}{2}$.
故选:B.
点评 此题考查了三角形内角和定理、三角形外角的性质以及角平分线的定义.此题难度较大,注意掌握整体思想与数形结合思想的应用.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题

| A. | 64 | B. | 60 | C. | 56 | D. | 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
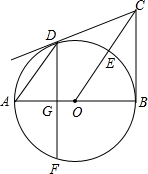 如图,AB是⊙O的直径,BC⊥AB于点B,连接OC、BD相交于点E,弦AD∥OC,弦DF⊥AB于点G.
如图,AB是⊙O的直径,BC⊥AB于点B,连接OC、BD相交于点E,弦AD∥OC,弦DF⊥AB于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x2+bx-c | B. | y=x2-bx+c | C. | y=-x2+bx+c | D. | y=-x2+bx-c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
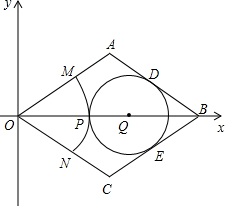 如图,菱形OABC的顶点O在坐标原点,顶点B在x轴的正半轴上,OA边所在直线为y=$\frac{\sqrt{3}}{3}$x,AB边所在直线为y=-$\frac{\sqrt{3}}{3}$x+2.
如图,菱形OABC的顶点O在坐标原点,顶点B在x轴的正半轴上,OA边所在直线为y=$\frac{\sqrt{3}}{3}$x,AB边所在直线为y=-$\frac{\sqrt{3}}{3}$x+2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com