
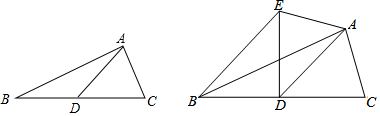
分析 (1)只要证明△BDE是等腰直角三角形即可解决问题;
(2)过E作EF⊥AD于F,求出EF,分别求出△BDE,△ADE的面积即可解决问题.
(3)△ADC为等腰直角三角形.只要证明CD=CA,即可解决问题.
解答 解:(1)由题意,得△AED≌△ACD,
∵∠ADC=45°,
∴∠ADE=45°,
∴∠EDB=∠EDC=∠ADC+∠ADE=90°,
∵AD为△ABC的中线,BC=12cm,
∴BD=CD=$\frac{1}{2}$BC=6cm,
∴DE=CD=6cm,
在Rt△BDE中,BE=$\sqrt{B{D}^{2}+D{E}^{2}}$=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$cm.
(2)过E作EF⊥AD于F,
∵∠ADE=45°,
∴△EDF为等腰直角三角形.
∴EF=$\frac{\sqrt{2}}{2}$ED
∵AD=8,
∴S△AED=$\frac{1}{2}$•AD•EF=$\frac{1}{2}$×8×3$\sqrt{2}$=12$\sqrt{2}$,
S△BED=$\frac{1}{2}$•BD•ED=18
∴S四边形AEBD=S△AED+S△BED=18+12$\sqrt{2}$(cm2).
(3)结论:△ADC为等腰直角三角形.
理由:若四边形AEBD是平行四边形,
∴AE∥BD,AE=BD,
∴AC=AE=BD=CD,
∵∠ADC=45°,
∴∠DAC=45°,
∴∠C=90°,
∴△ADC为等腰直角三角形.
点评 本题考查四边形综合题、等腰直角三角形的性质、勾股定理、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
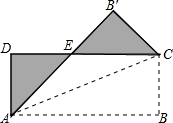 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为( )
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E,若AB=8,AD=3,则图中阴影部分的周长为( )| A. | 16 | B. | 19 | C. | 22 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚硬币,着地时反面向上 | |
| B. | 买一张福利彩票中奖了 | |
| C. | 投掷3枚骰子,面朝上的三个数字之和为18 | |
| D. | 五边形的内角和为540度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一批手机电池的使用寿命 | B. | 你所在学校的男、女同学的人数 | ||
| C. | 中国公民保护环境的意识 | D. | 端午节期间泰兴市场上粽子的质量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
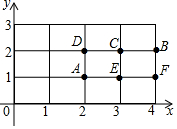 如图,若用A(2,1)表示放置2个胡萝卜,1棵小白菜;点B(4,2)表示放置4个胡萝卜,2棵小白菜:
如图,若用A(2,1)表示放置2个胡萝卜,1棵小白菜;点B(4,2)表示放置4个胡萝卜,2棵小白菜:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
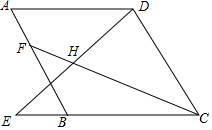 如图,在?ABCD中,AD=CD,AB=14.点E在CB的延长线上,点F在AB边上,连接DE、CF相交于点H,若∠CHD=∠A.BF=11,CF=20,则线段BE的长为$\frac{35}{11}$.
如图,在?ABCD中,AD=CD,AB=14.点E在CB的延长线上,点F在AB边上,连接DE、CF相交于点H,若∠CHD=∠A.BF=11,CF=20,则线段BE的长为$\frac{35}{11}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com