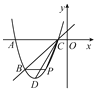
【题目】如图，已知抛物线y=ax2＋bx＋5经过A(－5，0)，B(－4，－3)两点，与x轴的另一个交点为C，顶点为D，连接CD．
（1）求该抛物线的解析式；
（2）点P为该抛物线上一动点(与点B，C不重合)，设点P的横坐标为t．当点P在直线BC的下方运动时，求△PBC的面积的最大值．
亮点激活精编提优100分大试卷系列答案
智趣寒假作业云南科技出版社系列答案科目：初中数学 来源： 题型：
【题目】春晓中学为开展“校园科技节”活动，计划购买A型、B型两种型号的航模．若购买8个A型航模和5个B型航模需用2200元；若购买4个A型航模和6个B型航模需用1520元．求A，B两种型号航模的单价分别是多少元．
查看答案和解析>>
科目：初中数学 来源： 题型：
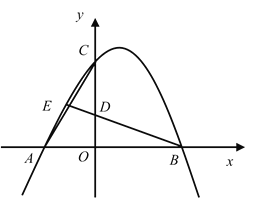
【题目】如图，已知抛物线
经过点
，
，
，点
为
中点，连接
、
，并延长交于点
．
（1）求抛物线的表达式；
（2）若抛物线与抛物线
关于
轴对称，在抛物线位于第二象限的部分上取一点
，过点作
轴，垂足为点
，是否存在这样的点，使得
与
相似？若存在，请求出点坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在四边形ABCD内接于⊙O，AB＝AC，BD为⊙O的直径，AE⊥BD，垂足为点E，交BC于点F．
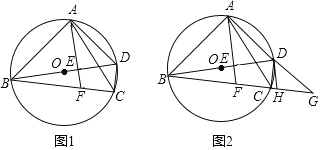
（1）求证：FA＝FB；
（2）如图2，分别延长AD，BC交于点G，点H为FG的中点，连接DH，若tan∠ACB＝
，求证：DH为⊙O的切线；
（3）在（2）的条件下，若DA＝3，求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y＝x2﹣2和x轴交于A，B（点A在点B右边）两点，和y轴交于点C，P为抛物线上的动点．
（1）求出A，C的坐标；
（2）求动点P到原点O的距离的最小值，并求此时点P的坐标；
（3）当点P在x轴下方的抛物线上运动时，过P的直线交x轴于E，若△POE和△POC全等，求此时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
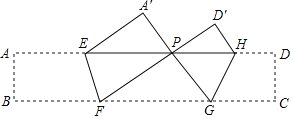
【题目】如图，把矩形ABCD沿EF，GH折叠，使点B，C落在AD上同一点P处，∠FPG＝90°，△A′EP的面积是8
，△D′PH的面积是4，则矩形ABCD的面积等于_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某宾馆有若干间标准房，当标准房的价格为200元时，每天入住的房间数为60间，经市场调查表明，该宾馆每间标准房的价格在170~240元之间（含170元，240元）浮动时，每天入住的房间数
（间）与每间标准房的价格
（元）的数据如下表：
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |
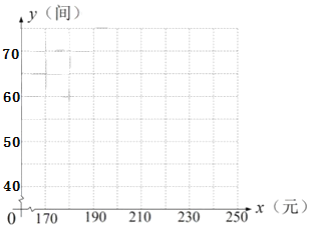
（1）根据所给数据在坐标系中描出相应的点，并画出图象.
（2）求关于的函数表达式、并写出自变量的取值范围.
（3）设客房的日营业额为
（元）.若不考虑其他因素，问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y＝ax2+bx+3经过点A（﹣1，0）、B（3，0）两点，且交y轴交于点C．
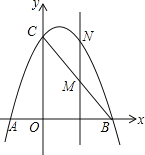
（1）求抛物线的解析式；
（2）点M是线段BC上的点（不与B、C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m，请用m的代数式表示MN的长；
（3）在（2）的条件下，连接NB，NC，是否存在点M，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点
（
，1）为函数
（
，
为常数，且
）与
的图象的交点.
（1）求；
（2）若函数的图象与
轴只有一个交点，求，；
（3）若
，设当
时，函数的最大值为
，最小值为
，求
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
