
【题目】下表列出了国外几个城市与首都北京的时差(带正号的表示同一时刻比北京时间早的时数),如北京时间的上午10:00时,东京时间的10点已过去了1小时,现在已是10+1=11:00.

(1)如果现在是北京时间8:00,那么现在的纽约时间是多少;
(2)此时(北京时间8:00)小明想给远在巴黎姑妈打电话,你认为合适吗?为什么?
(3)如果现在是芝加哥时间上午6:00,那么现在北京时间是多少?
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
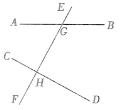
【题目】如图,直线AB,CD被直线EF所截,交点分别为G,H, ∠CHG=∠DHG=![]() ∠AGE.
∠AGE.
(1)CD与EF有怎样的位置关系?请说明理由.
(2)求∠CHG的同位角、内错角、同旁内角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
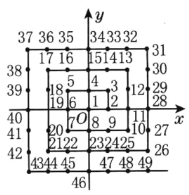
【题目】将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x,y均为整数,如数5对应的坐标为(-1,1),试探求2015对应的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C与某建筑物底端B相距306米(点C与点B在同一水平面上),某同学从点C出发,沿同一剖面的斜坡CD行走195米至坡顶D处,斜坡CD的坡度(或坡比)i=1:2.4,在D处测得该建筑物顶端A的俯视角为20°,则建筑物AB的高度约为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )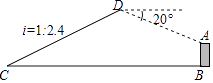
A.29.1米
B.31.9米
C.45.9米
D.95.9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,平移三角形ABC,使点A平移到点![]() ,画出平移后的三角形
,画出平移后的三角形![]() ;
;
(2)在(1)的条件下,指出点A,B,C 的对应点,并指出AB,BC,AC的对应线段和∠A,∠B, ∠C的对应角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0)、B(4,0)、C(0,2)三点.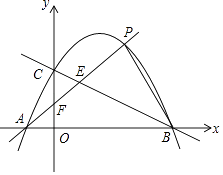
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2 , 求S1﹣S2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与双曲线y= ![]() (m≠0)相交于A(1,2),B(n,﹣1)两点.
(m≠0)相交于A(1,2),B(n,﹣1)两点. 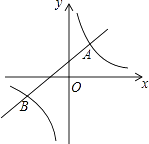
(1)求双曲线的解析式;
(2)若A1(x1 , y1),A2(x2 , y2),A3(x3 , y3)为双曲线上的三点,且x1<0<x2<x3 , 请直接写出y1 , y2 , y3的大小关系;
(3)观察图象,请直接写出不等式kx+b< ![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com