
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚筒轮⊙A,⊙A与水平地面相切于点D,在拉杆伸长到最大的情况下,当点B距离水平地面34cm时,点C到水平地面的距离CE为55cm.设AF∥ MN.

(1)求⊙A的半径.
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为76cm,∠CAF=64°,求此时拉杆BC的伸长距离(结果精确到1cm,参考数据:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图四边形OACB是菱形,OB在X轴的正半轴上,sin∠AOB=![]() .反比例函数y=
.反比例函数y=![]() 在第一象限图象经过点A,与BC交于点F.S△AOF=
在第一象限图象经过点A,与BC交于点F.S△AOF=![]() ,则k=( )
,则k=( )

A. 15 B. 13 C. 12 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 是等边三角形,点 D、E 分别在 BC、AC 上,且 BD=![]() BC,CE=
BC,CE= ![]() AC,BE、AD 相交于点 F,连接 DE, 则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DFDA;④AFBE=AEAC,正确的结论有( )
AC,BE、AD 相交于点 F,连接 DE, 则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DFDA;④AFBE=AEAC,正确的结论有( )
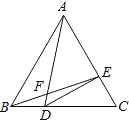
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是_____.
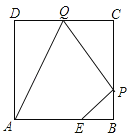
查看答案和解析>>
科目:初中数学 来源: 题型:
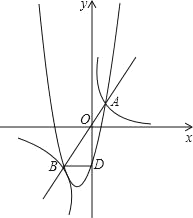
【题目】如图,直角坐标系中y=mx和![]() (m>0)图象的交点为A、B,BD⊥y轴于D,S△ABD=4;直线A′B′由直线AB缓慢向下平移;
(m>0)图象的交点为A、B,BD⊥y轴于D,S△ABD=4;直线A′B′由直线AB缓慢向下平移;
(1)求m的值;
(2)问直线A′B′向下平移多少单位时与经过B、D、A三点的抛物线刚好只有一个交点,并求出交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,若已知
,若已知![]() 点的坐标为
点的坐标为![]() .
.
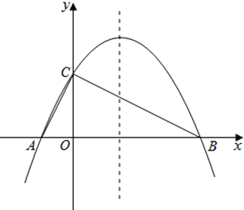
(1)求抛物线的解析式;
(2)求线段![]() 所在直线的解析式;
所在直线的解析式;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,求出符合条件的
为等腰三角形?若存在,求出符合条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米;上面五层居住,每层高度相等,测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米,求居民楼的高度.(精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和点C,与y轴交于点B,
和点C,与y轴交于点B,![]() 的面积是6.
的面积是6.
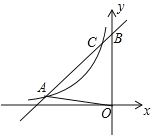
(1)求一次函数与反比例函数的表达式;(2)当![]() 时,比较
时,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com