
分析 (1)方程两边同乘最简公分母(2x-1),去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)把x=1代入方程mx+n=-2求出m+n=-2,根据完全平方公式代入求出即可.
解答 解:(1)去分母,方程两边同乘最简公分母(2x-1),得:2x-5=3(2x-1),
解得x=-$\frac{1}{2}$,
经检验x=-$\frac{1}{2}$是原方程的解,
所以原方程的解为x=-$\frac{1}{2}$;
(2)∵x=1是方程mx+n=-2的解,
∴m+n=-2,
∴2m2+4mn+2n2-6
=2(m+n)2-6
=2×(-2)2-6
=2.
点评 此题考查了(1)解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根;
(2)因式分解、完全平方公式和一元一次方程的解的应用,关键是求出m+n的值.


科目:初中数学 来源: 题型:解答题
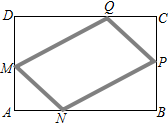 在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=x m,已知矩形的边BC=200m,边AB=a m,a为大于200的常数,设四边形MNPQ的面积为sm2
在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=x m,已知矩形的边BC=200m,边AB=a m,a为大于200的常数,设四边形MNPQ的面积为sm2查看答案和解析>>
科目:初中数学 来源: 题型:解答题
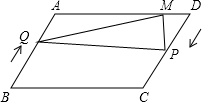 已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).
已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
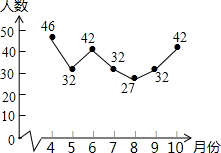 在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )
在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )| A. | 46人 | B. | 42人 | C. | 32人 | D. | 27人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
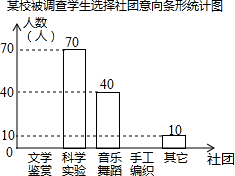 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 所占百分比 |
| 文学鉴赏 | a |
| 科学实验 | 35% |
| 音乐舞蹈 | b |
| 手工编织 | 10% |
| 其他 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com