
【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C处与地面的距离.(结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
【答案】解:过C点作AB的垂线交AB的延长线于点D,
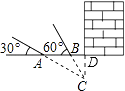
∵∠CAD=30°,∠CBD=60°,
∴∠ACB=30°,
∴∠CAB=∠ACB=30°,
∴BC=AB=4米,
在Rt△CDB中,BC=4米,∠CBD=60°,sin∠CBD= ![]() ,
,
∴sin60°= ![]() ,
,
∴CD=4sin60°=4× ![]() =2
=2 ![]() ≈3.5(米),
≈3.5(米),
故该生命迹象所在位置的深度约为3.5米.
【解析】本题考查的是解直角三角形的应用,先根据题意先过C点作AB的垂线交AB的延长线于点D,由三角形外角的性质可得出∠ACB=30°,进而可得出BC=AB=4米,在Rt△CDB中利用锐角三角函数的定义即可求出CD的值.
【考点精析】根据题目的已知条件,利用关于坡度坡角问题的相关知识可以得到问题的答案,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F. 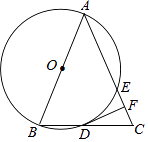
(1)求证:DF是⊙O的切线;
(2)若AE=4,cosA= ![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
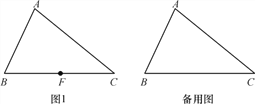
【题目】已知三角形ABC,EF∥AC交直线AB于点E,DF∥AB交直线AC于点D.
(1)如图1,若点F在边BC上,
①补全图形;
②判断∠BAC与∠EFD的数量关系,并给予证明;
(2)若点F在边BC的延长线上,(1)中的结论还成立吗?若成立,给予证明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲骑自行车从
两地,甲骑自行车从![]() 地到
地到![]() 地;乙骑自行车从
地;乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回,如图是甲乙两人离
地后立即按原路返回,如图是甲乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图像,根据图像解答以下问题:
之间的函数图像,根据图像解答以下问题:
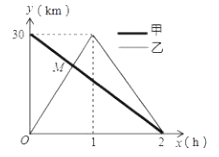
(1)求出甲离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数表达式;
之间的函数表达式;
(2)求出点![]() 的坐标,并解释改点坐标所表示的实际意义;
的坐标,并解释改点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过![]() 时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时
时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持练习时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=﹣x+1(0≤x≤10)与反比例函数y= ![]() (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
(﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )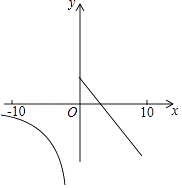
A.﹣ ![]() ≤x≤1
≤x≤1
B.﹣ ![]() ≤x≤
≤x≤ ![]()
C.﹣ ![]() ≤x≤
≤x≤ ![]()
D.1≤x≤ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
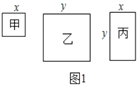
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为![]() 的正方形,乙种纸片是边长为
的正方形,乙种纸片是边长为![]() 的正方形,丙种纸片是长为
的正方形,丙种纸片是长为![]() ,宽为
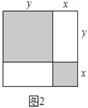
,宽为![]() 的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
(理解应用)
(1)观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
(拓展升华)
(2)利用(1)中的等式解决下列问题.
①已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com