
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA=2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm.

科目:初中数学 来源: 题型:
【题目】背景资料:
在已知△ABC所在平面上求一点P,使它到三角形的三个顶点的距离之和最小.
这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的,所求的点被人们称为“费马点”.
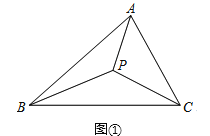
如图①,当△ABC三个内角均小于120°时,费马点P在△ABC内部,此时∠APB=∠BPC=∠CPA=120°,此时,PA+PB+PC的值最小.
解决问题:
(1)如图②,等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA,PB,PC转化到一个三角形中,从而求出∠APB= ;
基本运用:
(2)请你利用第(1)题的解答思想方法,解答下面问题:
如图③,△ABC中,∠CAB=90°,AB=AC,E,F为BC上的点,且∠EAF=45°,判断BE,EF,FC之间的数量关系并证明;
能力提升:
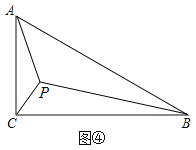
(3)如图④,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点P为Rt△ABC的费马点,
连接AP,BP,CP,求PA+PB+PC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
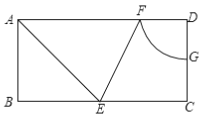
【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
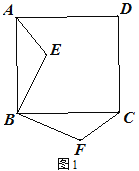
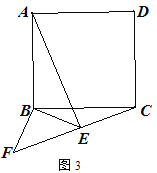
【题目】已知正方形ABC D,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.
(1)如图1,求证:①![]() ;②
;②![]() .
.
(2)若![]() ,
,
① 如图2,点E在正方形内,连接EC,若![]() ,
, ![]() ,求
,求![]() 的长;
的长;
② 如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,
求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=4,以A为圆心,3为半径作圆.试判断:
①点C与⊙A的位置关系;②点B与⊙A的位置关系;③AB中的D点与⊙A的位置关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(m,n),且满足m-2+(n-2)2=0,过A作AB⊥y轴,垂足为B.
(1)求A点坐标;
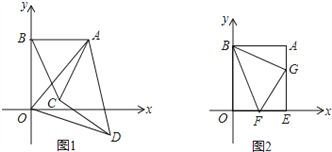
(2)如图1,分别以AB,AO为边作等边△ABC和△AOD,试判定线段AC和DC的数量关系和位置关系,并说明理由;
(3)如图2,过A作AE⊥x轴,垂足为E,点F、G分别为线段OE、AE上的两个动点 (不与端点重合),满足∠FBG=45°,设OF=a,AG=b,FG=c,试探究![]() 的值是 否为定值?如果是,直接写出此定值:如果不是,请举例说明.
的值是 否为定值?如果是,直接写出此定值:如果不是,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家窗户上的遮雨罩是一种玻璃钢制品,它的顶部是圆柱侧面的一部分(如图),它的侧面边缘上有两条圆弧(如图3),其中顶部圆弧![]() 的圆心
的圆心![]() 在竖直边缘
在竖直边缘![]() 上,另一条圆弧
上,另一条圆弧![]() 的圆心
的圆心![]() 在水平边缘
在水平边缘![]() 的延长线上,其圆心角为90°,请你根据所标示的尺寸(单位:cm)解决下面的问题(玻璃钢材料的厚度忽略不计,
的延长线上,其圆心角为90°,请你根据所标示的尺寸(单位:cm)解决下面的问题(玻璃钢材料的厚度忽略不计, ![]() 取3.1416).
取3.1416).
(1)计算出弧![]() 所对的圆心角的度数(精确到0.01度)及弧
所对的圆心角的度数(精确到0.01度)及弧![]() 的长度(精确到0.1cm);
的长度(精确到0.1cm);
(2)计算出遮雨罩一个侧面的面积(精确到1cm2);
(3)制做这个遮雨罩大约需要多少平方米的玻璃钢材料(精确到0.1平方米)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于( )
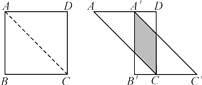
A. 4 cm B. 8 cm C. 6 cm D. 4 cm或8 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,林老师给出了下列方框中的一道题:
小聪和同桌小明讨论后,得出如下解答:
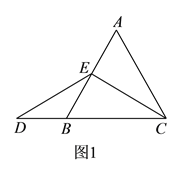
(![]() )特殊情况,探索结论
)特殊情况,探索结论
当点![]() 为
为![]() 的中点时,如图
的中点时,如图![]() ,确定线段
,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论: ![]() ______
______ ![]() (填“
(填“![]() ”“
”“ ![]() ”或“
”或“![]() ”).
”).
(![]() )特例启发,解答问题
)特例启发,解答问题
解:题目中, ![]() 与
与![]() 的大小关系是
的大小关系是![]() __________
__________ ![]() (填“
(填“![]() ”“
”“ ![]() ”或“
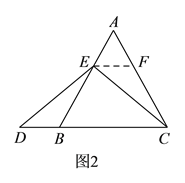
”或“![]() ”),理由如下:如图
”),理由如下:如图![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,(请你继续完成接下来的解题过程).
,(请你继续完成接下来的解题过程).
(![]() )拓展讨论,设计新题
)拓展讨论,设计新题
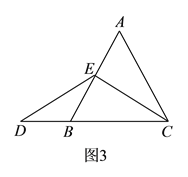
①互换林老师所给题的条件和结论,即:如图![]() 在等边三角形
在等边三角形![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,试确定线段
,试确定线段![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
②在等边三角形![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,若
,若![]() 的边长为
的边长为![]() ,
, ![]() ,求
,求![]() 的长为__________(请你直接写出结果).
的长为__________(请你直接写出结果).
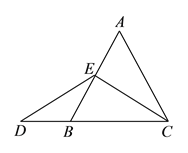
如图,在等边三角形![]() 中,点
中,点![]() 在
在![]()
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,
试确定线段![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com