
分析 根据a2+b2=39,ab=18,可求出(a+b)2和(a-b)2的值,进而求出(a+b)和(a-b)的值,然后代入[(a+b)(a-b)]2求解即可.
解答 解:∵a2+b2=39,ab=18,
∴(a+b)2=a2+b2+2ab=39+2×18=75,
(a-b)2=a2+b2-2ab=39-2×18=3,
∴(a+b)=$\sqrt{75}$=5$\sqrt{3}$,
(a-b)=$\sqrt{3}$,
∴[(a+b)(a-b)]2=[5$\sqrt{3}$×$\sqrt{3}$]2=225.
故答案为:225.
点评 本题考查了平方差公式,解答本题根据a2+b2=39,ab=18,求出(a+b)2和(a-b)2的值,进而求出(a+b)和(a-b)的值,然后代入[(a+b)(a-b)]2求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
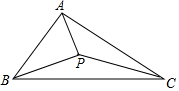 如图,△ABC 的角平分线交于点 P,已知 AB,BC,CA 的长分别为 5,7,6,则 S△ABP:S△BPC:S△APC=5:7:6.
如图,△ABC 的角平分线交于点 P,已知 AB,BC,CA 的长分别为 5,7,6,则 S△ABP:S△BPC:S△APC=5:7:6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com