
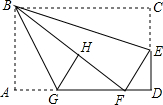
 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由折叠性质得∠1=∠2,CE=FE,BF=BC=10,则在Rt△ABF中利用勾股定理可计算出AF=8,所以DF=AD-AF=2,设EF=x,则CE=x,DE=CD-CE=6-x,在Rt△DEF中利用勾股定理得(6-x)2+22=x2,解得x=$\frac{10}{3}$,即ED=$\frac{8}{3}$;再利用折叠性质得∠3=∠4,BH=BA=6,AG=HG,易得∠2+∠3=45°,于是可对①进行判断;设AG=y,则GH=y,GF=8-y,在Rt△HGF中利用勾股定理得到y2+42=(8-y)2,解得y=3,则AG=GH=3,GF=5,由于∠A=∠D和 $\frac{AB}{DE}$≠$\frac{AG}{DF}$,可判断△ABG与△DEF不相似,则可对②进行判断;根据三角形面积公式可对③进行判断;利用AG=3,GF=5,DF=2可对④进行判断.
解答 解:∵△BCE沿BE折叠,点C恰落在边AD上的点F处,
∴∠1=∠2,CE=FE,BF=BC=10,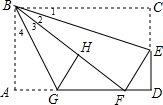
在Rt△ABF中,∵AB=6,BF=10,
∴AF=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴DF=AD-AF=10-8=2,
设EF=x,则CE=x,DE=CD-CE=6-x,
在Rt△DEF中,∵DE2+DF2=EF2,
∴(6-x)2+22=x2,解得x=$\frac{10}{3}$,
∴ED=$\frac{8}{3}$,
∵△ABG沿BG折叠,点A恰落在线段BF上的点H处,
∴∠3=∠4,BH=BA=6,AG=HG,
∴∠2+∠3=$\frac{1}{2}$∠ABC=45°,所以①正确;
HF=BF-BH=10-6=4,
设AG=y,则GH=y,GF=8-y,
在Rt△HGF中,∵GH2+HF2=GF2,
∴y2+42=(8-y)2,解得y=3,
∴AG=GH=3,GF=5,
∵∠A=∠D,$\frac{AB}{DE}$=$\frac{6}{\frac{8}{3}}$=$\frac{9}{4}$,$\frac{AG}{DF}$=$\frac{3}{2}$,
∴$\frac{AB}{DE}$≠$\frac{AG}{DF}$,
∴△ABG与△DEF不相似,所以②错误;
∵S△ABG=$\frac{1}{2}$•6•3=9,S△FGH=$\frac{1}{2}$•GH•HF=$\frac{1}{2}$×3×4=6,
∴S△ABG=$\frac{3}{2}$S△FGH,所以③错误;
∵AG+DF=3+2=5,而GF=5,
∴AG+DF=GF,所以④正确.
∴①④正确.
故选B.
点评 本题考查的是相似三角形的判定与性质,熟练掌握折叠和矩形的性质、相似三角形的判定方法;会运用勾股定理计算线段的长.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:填空题
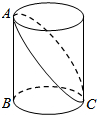 如图,已知圆柱底面周长是4dm,圆柱的高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为2$\sqrt{13}$dm.
如图,已知圆柱底面周长是4dm,圆柱的高为3dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为2$\sqrt{13}$dm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 400元 | B. | 440元 | C. | 320元 | D. | 270元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
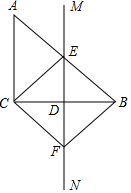 如图,在直角△ABC中,∠ACB=90°,BC的垂直平分线MN交BC于点D,交AB于点E,CF∥AB交MN于点F,连接CE、BF.
如图,在直角△ABC中,∠ACB=90°,BC的垂直平分线MN交BC于点D,交AB于点E,CF∥AB交MN于点F,连接CE、BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
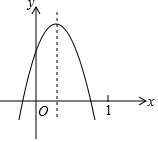 已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:
已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com