
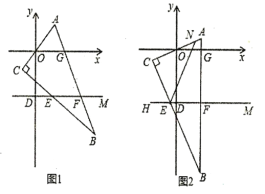
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 平行于
平行于![]() 轴并交
轴并交![]() 轴于
轴于![]() ,一块三角板摆放其中,其边与
,一块三角板摆放其中,其边与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与直线
两点,与直线![]() 分别交于
分别交于![]() ,
,![]() 两点,
两点,
(1)将三角板如图1所示的位置摆放,请写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(2)将三角板按如图2所示的位置摆放,![]() 为
为![]() 上一点,
上一点,![]() ,请写出
,请写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)![]() ;(2)∠NEF+∠AOG=90°
;(2)∠NEF+∠AOG=90°
【解析】
(1)延长AC交直线DM于点P,通过平行线的性质得出∠AOG=∠APD,再由垂直关系得出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(2)延长AC交直线DM于点Q,通过平行线的性质得出∠AOG=∠AQD,再根据![]() 及垂直关系得出
及垂直关系得出![]() 与
与![]() 之间的数量关系即可.
之间的数量关系即可.
解:(1)如图,延长AC交直线DM于点P,
∵DM∥x轴,
∴∠AOG=∠APD,
又∵∠ACB=90°
∴∠PCB=90°,
∴∠APD+∠CEP=90°,
又∵∠CEF+∠CEP=180°,
∴∠CEF-∠APD=90°,
即![]() .
.
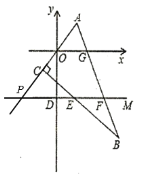
(2)如图,延长AC交直线DM于点Q,
∵DM∥x轴,
∴∠AOG=∠AQD,
又∵∠ACB=90°
∴∠QCB=90°,
∴∠AQD+∠CEQ=90°,
又∵![]()
∠CEQ+∠CEF=180°
∴∠NED=∠CEQ,
∴∠NED+∠AQD=90°,
即∠NEF+∠AOG=90°.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2cm,AB=4cm,动点P从点C出发,在BC边上以每秒![]() cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C→A→B以每秒4cm的速度匀速运动,运动时间为t秒
cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C→A→B以每秒4cm的速度匀速运动,运动时间为t秒![]() ,连接PQ,以PQ为直径作⊙O.
,连接PQ,以PQ为直径作⊙O.
(1)当![]() 时,求△PCQ的面积;
时,求△PCQ的面积;
(2)设⊙O的面积为s,求s与t的函数关系式;
(3)当点Q在AB上运动时,⊙O与Rt△ABC的一边相切,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
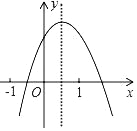
【题目】二次函数y=ax2+bx+c的图象如图示,下列结论:
(1)b<0;(2)c>0;(3)b2﹣4ac>0; (4)a﹣b+c<0,
(5)2a+b<0; (6)abc>0;其中正确的是_____;(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)随气体体积V(单位:立方米)的变化而变化,p随V的变化情况如表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出一个符合表格数据的p关于V的函数解析式
(2)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数解析式,基于安全考虑,气球的体积至少为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A
(a>0,b<0)的图象与x轴只有一个公共点A
(1)当a=![]() 时,求点A的坐标;
时,求点A的坐标;
(2)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥﹣1时,求点B的横坐标m的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,
作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A.11+![]() B.11-
B.11-![]()
C.11+![]() 或11-
或11-![]() D.11-
D.11-![]() 或1+
或1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
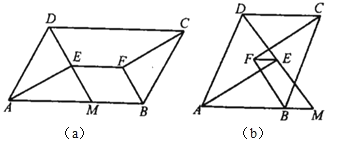
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,
,![]() 与
与![]() 的平分线交于
的平分线交于![]() 点,连接
点,连接![]() .
.
(1)延长![]() 交
交![]() 于
于![]() 点,则图(a)中与线段
点,则图(a)中与线段![]() 一定相等的线段有哪几条?说明理由(不再另外添加字母和辅助线).
一定相等的线段有哪几条?说明理由(不再另外添加字母和辅助线).
(2)![]() 、
、![]() 与
与![]() 之间有怎样的数量关系?为什么?
之间有怎样的数量关系?为什么?
(3)如果将条件“![]() ”改为“
”改为“![]() ”,如图(b)所示,其他条件不变,
”,如图(b)所示,其他条件不变,![]() 、
、![]() 与
与![]() 的关系又如何?直接写出结论.
的关系又如何?直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形, D、 E分别在边AB、AC上,且AD=CE,CD与BE相交于点O.
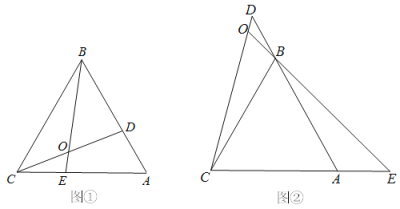
(1)如图①,求∠BOD的度数;
(2)如图②,如果点D、 E分别在边AB、CA的延长线上时,且AD=CE,求∠BOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com