
 轴上,点C与原点重合,CD=4,BC=9,在点P运动的同时,矩形ABCD沿x轴向右以每秒1个单位长的速度运动.
轴上,点C与原点重合,CD=4,BC=9,在点P运动的同时,矩形ABCD沿x轴向右以每秒1个单位长的速度运动.
|
|
| b |
| 2a |
| 4ac-b2 |
| 4a |
| 4×(-1)×(-32)-122 |
| 4×(-1) |
| 16 |
| 4 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•葫芦岛二模)如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x 轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
(2012•葫芦岛二模)如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x 轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
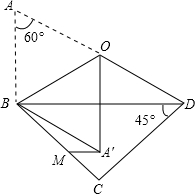 (2012•葫芦岛二模)如图,一副三角纸板拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为
(2012•葫芦岛二模)如图,一副三角纸板拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为| 6 |
| 2 |
| 6 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com