
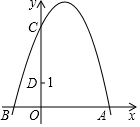
 如图,抛物线y=-x2+bx+c与x轴交于A(3,0)、B(-1,0),与y轴交于点C,
如图,抛物线y=-x2+bx+c与x轴交于A(3,0)、B(-1,0),与y轴交于点C,分析 (1)直接将A(3,0)、B(-1,0),代入函数解析式进而得出答案;
(2)当△PCD是以CD为底的等腰三角形时,则P点在线段CD的垂直平分线上,由C、D坐标可求得线段CD中点的坐标,从而可知P点的纵坐标,代入抛物线解析式可求得P点坐标.
解答 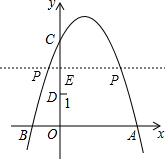 解:(1)∵抛物线y=-x2+bx+c与x轴交于A(3,0)、B(-1,0),
解:(1)∵抛物线y=-x2+bx+c与x轴交于A(3,0)、B(-1,0),
∴$\left\{\begin{array}{l}{-9+3b+c=0}\\{-1-b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线y=-x2+bx+c的解析式为:y=-x2+2x+3;
(2)∵△PCD是以CD为底的等腰三角形,
∴点P在线段CD的垂直平分线上,
如图,过P作PE⊥y轴于点E,则E为线段CD的中点,
∵抛物线y=-x2+2x+3与y轴交于点C,
∴C(0,3),且D(0,1),
∴E点坐标为(0,2),
∴P点纵坐标为2,
在y=-x2+2x+3中,令y=2,可得-x2+2x+3=2,
解得:x=1±$\sqrt{2}$,
∴P点坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
点评 本题主要考查了待定系数求二次函数解析式以及等腰三角形的性质,利用等腰三角形的性质求得P点纵坐标是解题的关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:选择题
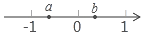 有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是( )
有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是( )| A. | 2 | B. | 0 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+(b-c)=a+b+c | B. | a-(b-c)=a-b-c | C. | a-(-b+c)=a-b-c | D. | a-(-b-c)=a+b+c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
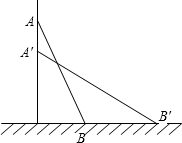 一架梯子长2.5米,斜靠在一面垂直于地面的墙上,梯子底端离墙0.7米.
一架梯子长2.5米,斜靠在一面垂直于地面的墙上,梯子底端离墙0.7米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-3x+1=0 | B. | $\frac{1}{{x}^{2}}$=0 | C. | ax2+bx+c=0 | D. | x+3=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,4,8 | B. | 8,15,7 | C. | 13,12,20 | D. | 5,5,11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com