练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在边长为正整数的△ABC中，AB=AC，且AB边上的中线CD将△ABC的周长分为1：2的两部分，则△ABC面积的最小值为（ ）
    A.
    B.
    C.
    D.

    【答案】C
    【解析】解：设这个等腰三角形的腰为x，底为y，分为的两部分边长分别为n和2n，得 或 ，
    解得 或 ，
    ∵2× ＜ （此时不能构成三角形，舍去）
    ∴取 ，其中n是3的倍数
    ∴三角形的面积S△= × × = n2 ， 对于S△= n2= n2 ，
    当n＞0时，S△随着n的增大而增大，故当n=3时，S△= 取最小．
    故选：C．
    【考点精析】认真审题，首先需要了解三角形的面积(三角形的面积=1/2×底×高)，还要掌握三角形三边关系(三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

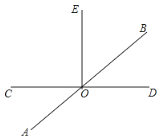
    【题目】如图，已知直线AB和CD相交于点O，在∠COB的内部作射线OE.

    （1）若∠AOC=36°，∠COE=90°，求∠BOE的度数；

    （2）若∠COE：∠EOB：∠BOD=4：3：2，求∠AOE的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

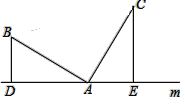
    【题目】问题发现：如图，已知：AB=AC，∠BAC=90°，直线m经过点A，过点B作BD⊥m于D， CE⊥m于E．我们把这种常见图形定义为“K”字图.很容易得到线段DE、BD、CE之间的数量关系是 .

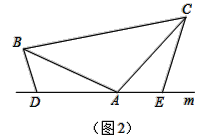
    拓展探究：如图2，若AB=AC，∠BAC=∠BDA=∠AEC，则线段DE、BD、CE之间的数量关系还成立吗？如果成立，请证明之.

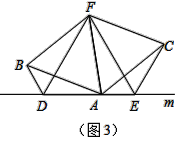
    解决问题：如图3，若AB=AC，∠BAC=∠BDA=∠AEC=120°，点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，BD=2，CE=4，求△DEF的周长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：2tan60°﹣| ﹣2|﹣ +（ ）﹣1 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“马航事件”的发生引起了我国政府的高度重视，迅速派出了舰船和飞机到相关海域进行搜寻．如图，在一次空中搜寻中，水平飞行的飞机观测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体（该物体视为静止）．为了便于观察，飞机继续向前飞行了800米到达B点，此时测得点F在点B俯角为45°的方向上，请你计算当飞机飞临F点的正上方点C时（点A、B、C在同一直线上），竖直高度CF约为多少米？（结果保留整数，参考数值： ≈1.7）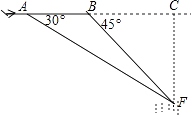

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD∥BC，∠A=90°，E是AB上的一点，且AD=BE，∠1=∠2．

    （1）求证：△ADE≌△BEC；

    （2）若AD=6，AB=14，请求出CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC，∠BAC=120，AD⊥BC，且AD=AB．

    （1）如图1，DE⊥AB，DF⊥AC，垂足分别为点E，F，求证：AE+AF=AD

    （2）如图2，如果∠EDF=60，且∠EDF两边分别交边AB，AC于点E，F，那么线段AE，AF，AD之间有怎样的数量关系？并给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．

    （1）求证：BE=CD；

    （2）连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．

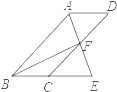
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，点A为线段BC外一动点，且BC=a，AB=b，填空：当点A位于　 　时，线段AC的长取到最大值，则最大值为　 ；（用含a、b的式子表示）。

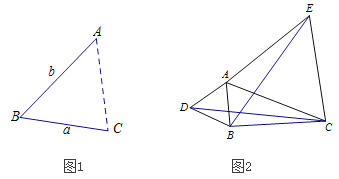
    （2）如图2，若点A为线段BC外一动点，且BC=4，AB=2，分别以AB，AC为边，作等边和等边，连接CD，BE.

    ①图中与线段BE相等的线段是线段 ，并说明理由；

    ②直接写出线段BE长的最大值为 。

    （3）如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，请直接写出线段AM长的最大值为 ，及此时点P的坐标为 。（提示：等腰直角三角形的三边长a、b、c满足a：b：c=1：1：）

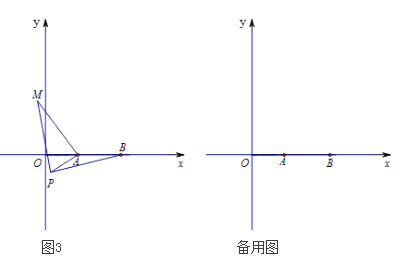
    查看答案和解析>>

    同步练习册答案