
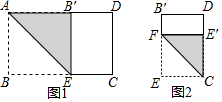
 矩形纸片ABCD中,AD=10,AB=a(5<a<10)
矩形纸片ABCD中,AD=10,AB=a(5<a<10)分析 首先根据题意可得可知当10<a<20时,第一次操作后剩下的矩形的长为a,宽为10-a,第二次操作时正方形的边长为10-a,第二次操作以后剩下的矩形的两边分别为10-a,2a-10.然后分别从10-a>2a-10与10-a<2a-10去分析求解,即可求得答案.
解答  解:由题意可知当5<a<10时,第一次操作后剩下的矩形的长为a,宽为10-a,
解:由题意可知当5<a<10时,第一次操作后剩下的矩形的长为a,宽为10-a,
所以第二次操作时剪下正方形的边长为10-a,第二次操作以后剩下的矩形的两边分别为10-a,2a-10;
∴E′D=2a-10;
此时,分两种情况:
①如果10-a>2a-10,即a<$\frac{20}{3}$,那么第三次操作时正方形的边长为2a-10.
则2a-10=(10-a)-(2a-10),解得a=6;
②如果10-a<2a-10,即a>$\frac{20}{3}$,那么第三次操作时正方形的边长为10-a.
则10-a=(2a-10)-(10-a),解得a=$\frac{15}{2}$.
∴当n=3时,a的值为2或$\frac{15}{2}$.
故答案为:2或$\frac{15}{2}$.
点评 此题考查了折叠的性质与矩形的性质.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用,注意折叠中的对应关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 25 | C. | 7 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成下面的证明.
完成下面的证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com