
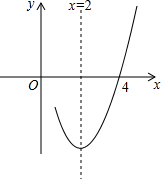
 已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:| A. | ①②③ | B. | ③④⑤ | C. | ①②④ | D. | ①④⑤ |
分析 ①由抛物线的对称轴结合抛物线与x轴的一个交点坐标,可求出另一交点坐标,结论①正确;②由抛物线对称轴为2以及抛物线过原点,即可得出b=-4a、c=0,即4a+b+c=0,结论②正确;③根据抛物线的对称性结合当x=5时y>0,即可得出a-b+c>0,结论③错误;④将x=2代入二次函数解析式中结合4a+b+c=0,即可求出抛物线的顶点坐标,结论④正确;⑤观察函数图象可知,当x<2时,yy随x增大而减小,结论⑤错误.综上即可得出结论.
解答 解:①∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),
∴抛物线与x轴的另一交点坐标为(0,0),结论①正确;
②∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线过原点,
∴-$\frac{b}{2a}$=2,c=0,
∴b=-4a,c=0,
∴4a+b+c=0,结论②正确;
③∵当x=-1和x=5时,y值相同,且均为正,
∴a-b+c>0,结论③错误;
④当x=2时,y=ax2+bx+c=4a+2b+c=(4a+b+c)+b=b,
∴抛物线的顶点坐标为(2,b),结论④正确;
⑤观察函数图象可知:当x<2时,y随x增大而减小,结论⑤错误.
综上所述,正确的结论有:①②④.
故选C.
点评 本题考查了抛物线与x轴的交点、二次函数图象与系数的关系以及二次函数图象上点的坐标特征,逐一分析五条结论的正误是解题的关键.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:选择题
| A. | y>10 | B. | 5<y<10 | C. | 1<y<2 | D. | 0<y<5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
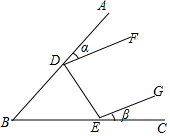 如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )
如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )| A. | α+β+γ=180 | B. | α+β=γ | C. | α+β+γ=90 | D. | 2α+2β-γ=45 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-(\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2})^{2}]}$.现已知△ABC的三边长分别为1,2,$\sqrt{5}$,则△ABC的面积为1.
我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-(\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2})^{2}]}$.现已知△ABC的三边长分别为1,2,$\sqrt{5}$,则△ABC的面积为1.查看答案和解析>>
科目:初中数学 来源:2017届江苏省启东市九年级寒假作业测试(开学考试)数学试卷(解析版) 题型:解答题
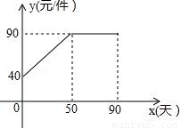
(本小题满分8分) 九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设
该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w
(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com