
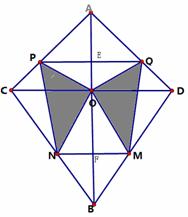
如图,AB垂直平分CD,AB与CD相交于点O,CD=2 cm,∠CAD=90°,∠CBD=60°,
点P、Q、M、N分别沿图示方向在线段上运动,同时开始以1cm/s的速度运动。
(1) 设出发时间为t(s)是否存在某一时刻,四边形PQMN为长方形,若存在,请证明时间;若不存在,请说明理由;
(2) 点P、Q、M、N分别与点O连结,图中阴影部分图形称为蝶形,求蝶形面积S关于t的函数关系式(0<t<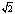 );
);
(3) 当t=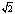 时,在AB上找一点G,使GQ+GM最小,画出图形并求此时OG的长。
时,在AB上找一点G,使GQ+GM最小,画出图形并求此时OG的长。
|
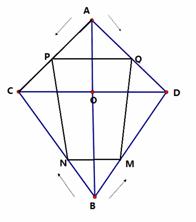
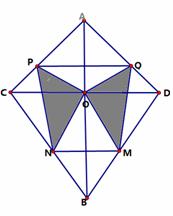
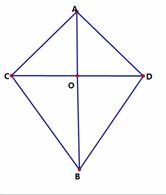 (1) (2) (3)
(1) (2) (3) (1)要是四边形成为长方形,证PQ=MN
∵AB垂直平分CD,
∴CO=DO
∵∠CAD=90°,∠CBD=60°,CD=2 cm
∴AO=CO=DO=1,BO=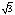 ,CB=DB=2 (直接利用相似也行)
,CB=DB=2 (直接利用相似也行)
∵AP=AQ=BM=BN= t
∴PQ=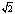 t,MN= t
t,MN= t
∴不存在某一时刻,四边形PQMN为长方形-
(2)如图作AB与PQ、MN交于点E、F
∵PQ=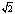 t,MN= t
t,MN= t
∴PE=QE= t,EO=1-
t,EO=1- t
t
MF=NF=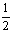 t,BF=
t,BF= t,FO=
t,FO=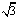 -
- t
t
S=S梯形PQMN-S△POQ-S△MON= -
-
(3)利用轴对称与两点之间线段
如图,M关于AB的对称点为N,P、Q与C、D重合,
连结NQ交AB与点G,此时GQ+GM最小
计算OG的长可以建立直角坐标系,求出NQ所在直线的函数与Y轴的交点G(0,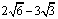 )
)
∴OG=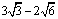 -
-



 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
一个不透明的口袋中有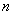 个小球,其中两个是白球,其余为红球,这些球的形状、大小、质地等完全相同,从袋中随机地取出一个球,它是红球的概率是
个小球,其中两个是白球,其余为红球,这些球的形状、大小、质地等完全相同,从袋中随机地取出一个球,它是红球的概率是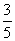 .
.
(1)求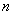 的值;
的值;
(2)把这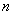 个球中的两个标号为1,其余分别标号为2,3,…,
个球中的两个标号为1,其余分别标号为2,3,…, ,随机地取出一个小球后不放回,再随机地取出一个小球,请用画树状图或列表的方法求第二次取出小球标号大于第一次取出小球标号的概率.
,随机地取出一个小球后不放回,再随机地取出一个小球,请用画树状图或列表的方法求第二次取出小球标号大于第一次取出小球标号的概率.
(3)在第(2)小题中若把两个标号为1的球分给甲、乙、丙三位同学,则甲乙各得一球的概率是多少?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
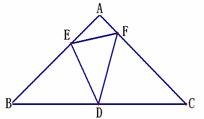
△ABC是等腰直角三角形,∠A=90°,AB=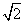 ,点D位 于 边BC的中点上.点E在AB上,点F在AC上,∠EDF=45°,给出以下结论:①当BE=1时,
,点D位 于 边BC的中点上.点E在AB上,点F在AC上,∠EDF=45°,给出以下结论:①当BE=1时,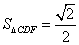 ; ②∠DFC=∠EDB;③CF×BE=1;④
; ②∠DFC=∠EDB;③CF×BE=1;④ ;⑤
;⑤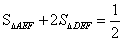 ;正确的有( )
;正确的有( )
A.①④⑤ B.①③④⑤ C. ②③④ D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
用9根相同的火柴棒拼成一个三角形,火柴棒不允许剩余、重叠和折断,则能摆出不同的三角形的个数是( )(初一天天伴习题改编)
(A)4种 (B) 3种 (C)2种 (D) 1种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com