
【题目】已知反比例函数y= ![]() ,当x>0时,y随x的增大而增大,则关于x的方程ax2﹣2x+b=0的根的情况是( )
,当x>0时,y随x的增大而增大,则关于x的方程ax2﹣2x+b=0的根的情况是( )
A.有两个正根
B.有两个负根
C.有一个正根一个负根
D.没有实数根
【答案】C
【解析】解:因为反比例函数y= ![]() ,当x>0时,y随x的增大而增大, 所以ab<0,
,当x>0时,y随x的增大而增大, 所以ab<0,
所以△=4﹣4ab>0,
所以方程有两个实数根,
再根据x1x2= ![]() <0,
<0,
故方程有一个正根和一个负根.
故选C.
【考点精析】掌握求根公式和根与系数的关系是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x﹣
x﹣ ![]() 与x,y轴分别交于点A,B,与反比例函数y=
与x,y轴分别交于点A,B,与反比例函数y= ![]() 的图象在第二象限交于点C,过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的坐标为 .
的图象在第二象限交于点C,过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的坐标为 . 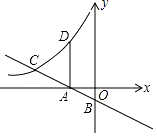
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF. 
(1)求证:EF∥平ABD面;
(2)若AE⊥平面BCD,BD⊥CD,求证:平面AEF⊥平面ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=﹣ ![]() (x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=
(x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y= ![]() (k>0,x>0)于点P,且OAMP=12.
(k>0,x>0)于点P,且OAMP=12.
(1)求k的值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC. 
(1)求证:AB=AC;
(2)若AB=4,BC=2 ![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P,A,C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E. 请问:△CDP与△PAE相似吗?如果相似,请写出证明过程.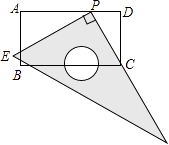
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D、E分别是AB、AC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③ ![]() .其中正确的有( )
.其中正确的有( ) 
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔40海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.问B处距离灯塔P有多远?(结果精确到0.1海里) (参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.449)
≈2.449)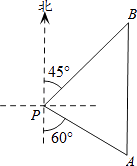
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com