
 如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2$\sqrt{3}$,则阴影部分的面积为$\frac{2π}{3}$.
如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2$\sqrt{3}$,则阴影部分的面积为$\frac{2π}{3}$. 分析 连接OD,则根据垂径定理可得出CE=DE,继而将阴影部分的面积转化为扇形OBD的面积,代入扇形的面积公式求解即可.
解答  解:连接OD.
解:连接OD.
∵CD⊥AB,
∴CE=DE=$\frac{1}{2}$CD=$\sqrt{3}$,
故S△OCE=S△ODE,即可得阴影部分的面积等于扇形OBD的面积,
又∵∠ABD=60°,
∴∠CDB=30°,
∴∠COB=60°,
∴OC=2,
∴S扇形OBD=$\frac{60π×{2}^{2}}{360}$=$\frac{2π}{3}$,即阴影部分的面积为$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查的是垂径定理,扇形的面积的计算,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | m<-2 | B. | m=-2 | C. | m<-1 | D. | -1≤m<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
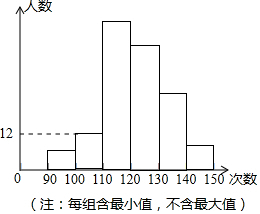 某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图(注:每组含最小值,不含最大值).甲同学计算出第二组的频率是0.06,乙同学计算出从左至右第一、二、三、四组的频数比为2:4:17:15.结合统计图回答下列问题:
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图(注:每组含最小值,不含最大值).甲同学计算出第二组的频率是0.06,乙同学计算出从左至右第一、二、三、四组的频数比为2:4:17:15.结合统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
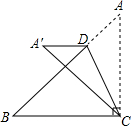 如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为4$\sqrt{2}$-4或4.
如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为4$\sqrt{2}$-4或4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系中,第一次将△OAB交换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).观察每次变换前后的三角形有何变化,按照变换规律,第五次变换后得到的三角形A5的坐标是(32,3),B5的坐标是(64,0),An的坐标是(2n,3).
如图,在直角坐标系中,第一次将△OAB交换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).观察每次变换前后的三角形有何变化,按照变换规律,第五次变换后得到的三角形A5的坐标是(32,3),B5的坐标是(64,0),An的坐标是(2n,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
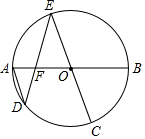 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,ED交AB于点F.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,ED交AB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com