
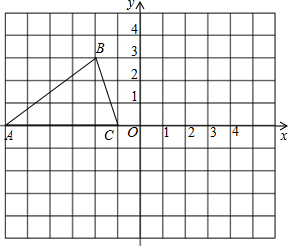
 如图,已知△ABC的三个顶点的坐标分别为A(-6,0)、B(-2,3)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-6,0)、B(-2,3)、C(-1,0).科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:解答题
在直角坐标系中,△ABC的三个顶点的位置如图所示.
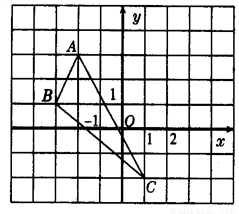
(1)请画出将△ABC先向右平移3个单位,再向上平移1个单位后得△A′B′C′,请在网格纸中画出△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′、B′、C′三点的坐标:A′_____,B′______,C′______.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
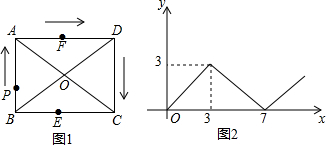 如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )
如图,矩形ABCD中,对角线AC,BD交于点O,E,F分别是边BC,AD的中点,AB=3,BC=4,一动点P从点B出发,沿着B-A-D-C在矩形的边上运动,运动到点C停止,点M为图1中某一定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.则点M的位置可能是图1中的( )| A. | 点C | B. | 点F | C. | 点D | D. | 点O |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,网格中每个小正方形的边长均为1个单位长度
如图,网格中每个小正方形的边长均为1个单位长度查看答案和解析>>
科目:初中数学 来源: 题型:填空题
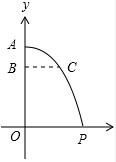 2008年7月某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口A,如图所示,如果空投物资离开A处后下落的垂直高度AB=160米时,它测A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高空进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为500米.
2008年7月某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口A,如图所示,如果空投物资离开A处后下落的垂直高度AB=160米时,它测A处的水平距离BC=200米,那么要使飞机在垂直高度AO=1000米的高空进行空投,物资恰好准确地落在居民点P处,飞机到P处的水平距离OP应为500米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
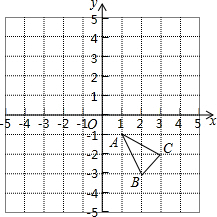 在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).
在如图所示的平面直角坐标系中,△ABC的三个顶点分别为A(1,-1),B(2,-3),C(3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
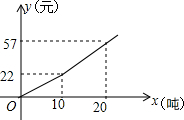 今年某市遭遇干旱,为鼓励市民节约用水,该市自来水公司按分段收费标准收费,如图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.
今年某市遭遇干旱,为鼓励市民节约用水,该市自来水公司按分段收费标准收费,如图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com