
【题目】已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.AD与BE平行吗?为什么?
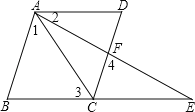
解:AD∥BE,理由如下:
∵AB∥CD(已知)
∴∠4= ( )
∵∠3=∠4(已知)
∴∠3= ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即 =
∴∠3= ( )
∴AD∥BE( )
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的对话。
小红:“售货员,我要买些梨。”
售货员说:“小红,你上次买的那种梨卖完了,我们还没来得及进货,我建议你这次买些新进的苹果,价格比梨贵一点,不过这批苹果的味道挺好哟!”
小红:“好,这次和上次一样,也花30元。”
对照前后两次的电脑小票,小红发现,每千克苹果的单价是梨的1.5倍,买的苹果的重量比梨轻2.5Kg。
试根据上面的对话和小红的发现,分别求出苹果和梨的单价。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() )与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.
)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.
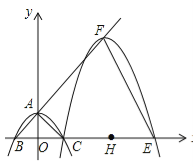
(1)求a、c的值及抛物线的解析式.
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4cm和6cm的两根小棒,请你再找一根小棒,并以这三根小棒为边围成一个三角形,下列长度的小棒可选的是( )
A. 1cm B. 2cm C. 7cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为假命题的个数有( )
①相等的角是对顶角;
②依次连结四边形四边中点所组成的图形是平行四边形;
③在同圆或等圆中,相等的弦所对的圆周角相等;
④在同圆中,平分弦的直径垂直于这条弦.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名工作人员,对甲、乙两位应聘者进行了笔试和面试,他们的成绩如下表所示:
候选人 | 测试成绩(百分制) | |
笔试 | 面试 | |
甲 | 95 | 85 |
乙 | 83 | 95 |
根据需要,笔试与面试的成绩按4:6的比例确定个人成绩(成绩高者被录用),那么谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.

(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5a3b·(-3b)2+(-ab)(-6ab)2;
(2)(x-3y)2+(3y-x)(x+3y);
(3)x(x2+3)+x2(x-3)-3x(x2-x-1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com