
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
(1)y=﹣x+3,y=x2﹣4x+3;(2)(0,0),(﹣3,0)或(0,﹣3);(3)存在,(4,3)或(﹣1,8).
解析试题分析:(1)由待定系数法求出直线BD和抛物线的解析式;
(2)首先确定△MCD为等腰直角三角形,因为△BND与△MCD相似,所以△BND也是等腰直角三角形.如答图1所示,符合条件的点N有3个;
(3)如答图2、答图3所示,解题关键是求出△PBD面积的表达式,然后根据S△PBD=6的已知条件,列出一元二次方程求解.
试题解析:(1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,∴A(﹣1,0),B(0,3).
∵把△AOB沿y轴翻折,点A落到点C,∴C(1,0).
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,∴ ,解得
,解得 .
.
∴直线BD的解析式为:y=﹣x+3.
设抛物线的解析式为:y=a(x﹣1)(x﹣3),
∵点B(0,3)在抛物线上,∴3=a×(﹣1)×(﹣3),解得:a=1.
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3.
(2)∵抛物线的解析式为:y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1).
直线BD:y=﹣x+3与抛物线的对称轴交于点M,令x=2,得y=1,∴M(2,1).
设对称轴与x轴交点为点F,则CF=FD=MN=1,∴△MCD为等腰直角三角形.
∵以点N、B、D为顶点的三角形与△MCD相似,∴△BND为等腰直角三角形.
如答图1所示:
(I)若BD为斜边,则易知此时直角顶点为原点O,∴N1(0,0).
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,∵OB=OD=ON2=3,∴N2(﹣3,0).
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,∵OB=OD=ON3=3,∴N3(0,﹣3).
∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3).
(3)存在,假设存在点P,使S△PBD=6,设点P坐标为(m,n),
(I)当点P位于直线BD上方时,如答图2所示,过点P作PE⊥x轴于点E,则PE=n,DE=m﹣3,
S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE= (3+n)•m﹣
(3+n)•m﹣ ×3×3﹣
×3×3﹣ (m﹣3)•n=6,化简得:m+n="7" ①.
(m﹣3)•n=6,化简得:m+n="7" ①.
∵P(m,n)在抛物线上,∴n=m2﹣4m+3,代入①式整理得:m2﹣3m﹣4=0,解得:m1=4,m2=﹣1.
∴n1=3,n2="8." ∴P1(4,3),P2(﹣1,8).
(II)当点P位于直线BD下方时,如答图3所示,过点P作PE⊥y轴于点E,
则PE=m,OE=﹣n,BE=3﹣n,
S△PBD=S梯形PEOD+S△BOD﹣S△PBE= (3+m)•(﹣n)+
(3+m)•(﹣n)+ ×3×3﹣
×3×3﹣ (3﹣n)•m=6,化简得:m+n=﹣1 ②.
(3﹣n)•m=6,化简得:m+n=﹣1 ②.
∵P(m,n)在抛物线上,∴n=m2﹣4m+3.
代入②式整理得:m2﹣3m+4=0,△=﹣7<0,此方程无解.∴此时点P不存在.
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8).
考点:1.二次函数综合题;2.翻折问题;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.等腰直角三角形的判定和性质;6.相似三角形的性质;7.解一元二次方程;8.图形面积计算;9.转换思想、数形结合思想和分类思想的应用.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
已知二次函数图像与y轴交于点(0,-4),并经过(-1,-6)和(1,2)
(1)求这个二次函数的解析式;
(2)求出这个函数的图像的开口方向,对称轴和顶点坐标;
(3)该函数图像与x轴的交点坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
矩形OABC在平面直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(0,3),直线 与BC边相交于点D.
与BC边相交于点D.
(1)求点D的坐标;
(2)若抛物线 经过A、D两点,试确定此抛物线的解析式;
经过A、D两点,试确定此抛物线的解析式;
(3)设(2)中的抛物线的对称轴与直线AD交于点M,点P为对称轴上一动点,以P、A、M为顶点的三角形与△ABD相似,求符合条件的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:二次函数y=x2-4x+3.
(1)将y=x2-4x+3化成 的形式;
的形式;
(2)求出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+2.6已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.
(1)求y与x的关系式;(不要求写出自变量x的取值范围)
(2)球能否越过球网?球会不会出界?请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
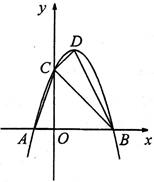
如图,抛物线 交
交 轴于
轴于 两点(
两点( 的左侧),交
的左侧),交 轴于点
轴于点 ,顶点为
,顶点为 。
。
(1)求点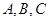 的坐标;
的坐标;
(2)求四边形 的面积;
的面积;
(3)抛物线上是否存在点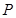 ,使得
,使得 ,若存在,请求出点
,若存在,请求出点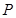 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线 交x轴于A点,交y轴于B点,抛物线
交x轴于A点,交y轴于B点,抛物线 经过点A、B,交x轴于另一点C,顶点为D.
经过点A、B,交x轴于另一点C,顶点为D.
(1)求抛物线的函数表达式;
(2)求点C、D两点的坐标;
(3)求△ABD的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点.
(2)设a<0,当此函数图象与x轴的两个交点的距离为 时,求出此二次函数的解析式.
时,求出此二次函数的解析式.
(3)在(2)的条件下,若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为 ,若存在求出P点坐标,若不存在请说明理由。
,若存在求出P点坐标,若不存在请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与
与 轴相交于点
轴相交于点 (﹣1,0)、
(﹣1,0)、 (3,0),与
(3,0),与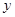 轴相交于点
轴相交于点 ,点
,点 为线段
为线段 上的动点(不与
上的动点(不与 、
、 重合),过点
重合),过点 垂直于
垂直于 轴的直线与抛物线及线段
轴的直线与抛物线及线段 分别交于点
分别交于点 、
、 ,点
,点 在
在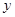 轴正半轴上,
轴正半轴上, =2,连接
=2,连接 、
、 .
.
(1)求抛物线的解析式;
(2)当四边形 是平行四边形时,求点
是平行四边形时,求点 的坐标;
的坐标;
(3)过点 的直线将(2)中的平行四边形
的直线将(2)中的平行四边形 分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com