
【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起.
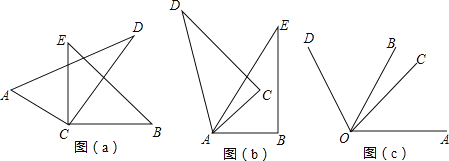
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
【答案】(1)145°,40°,∠ACB+∠DCE=180°,理由见解析;(2)∠DAB+∠CAE=120°,理由见解析;(3)∠AOD+∠BOC=α+β.
【解析】
(1)若∠DCE=35°,根据90°计算∠ACE的度数,再计算∠ACB的度数;若∠ACB=140°,同理,反之计算可得结果;先计算∠ACB=90°+∠BCD,再加上∠DCE可得∠ACB与∠DCE的关系;
(2)先计算∠DAB=60°+∠CAB,再加上∠CAE可得结果;
(3)先计算∠AOD=β+∠COA,再加上∠BOC可得结果.
解:(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=140°,
∵∠BCE=90°,
∴∠ACE=140°90°=50°,
∵∠ACD=90°,
∴∠DCE=90°50°=40°,
故答案为:145°;40°;
∠ACB+∠DCE=180°,
理由:∵∠ACB=∠ACD+∠BCD=90°+∠BCD,
∴∠ACB+∠DCE=90°+∠BCD+∠DCE=90°+∠BCE=180°;
(2)∠DAB+∠CAE=120°,
理由:∵∠DAB=∠DAC+∠CAB=60°+∠CAB,
∴∠DAB+∠CAE=60°+∠CAB+∠CAE=60°+∠EAB=120°;
(3)∠AOD+∠BOC=α+β,
理由:∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC=β+∠AOB=α+β.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,观察函数y=|x|的图象,写出它的两条的性质;
(2)在图1中,画出函数y=|x-3|的图象;
根据图象判断:函数y=|x-3|的图象可以由y=|x|的图象向 平移 个单位得到;
(3)①函数y=|2x+3|的图象可以由y=|2x|的图象向 平移 单位得到;
②根据从特殊到一般的研究方法,函数y=|kx+3|(k为常数,k≠0)的图象可以由函数y=|kx|(k为常数,k≠0)的图象经过怎样的平移得到.
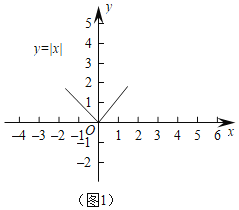
查看答案和解析>>
科目:初中数学 来源: 题型:
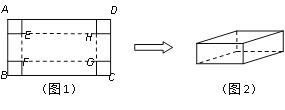
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为“方便交通,绿色出行”,人们常选择以共享单车作为代步工具、图(1)所示的是一辆自行车的实物图.图(2)是这辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45cm和60cm,且它们互相垂直,座杆CE的长为20cm.点A、C、E在同一条直线上,且∠CAB=75°.
(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732)
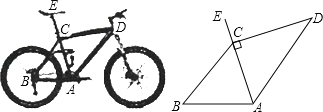
图(1) 图(2)
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习反比例函数后,为研究新函数![]() ,先将函数变形为
,先将函数变形为![]() ,画图发现函数
,画图发现函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象向上平移1个单位得到.
的图象向上平移1个单位得到.
(1)根据小明的发现,请你写出函数![]() 的图象可以由反比例函数
的图象可以由反比例函数![]() 的图象经过怎样的平移得到;
的图象经过怎样的平移得到;
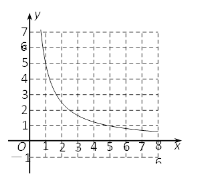
(2)在平面直角坐标系中,已知反比例函数![]() (x>0)的图象如图所示,请在此坐标系中画出函数
(x>0)的图象如图所示,请在此坐标系中画出函数![]() (x>0)的图象;
(x>0)的图象;
(3)若直线y=-x+b与函数![]() (x>0)的图象没有交点,求b的取值范围.
(x>0)的图象没有交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,……排成如下表:如图所示,图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数.
1 | 3 | 5 | 7 | 9 |
11 | 13 | 15 | 17 | 19 |
21 | 23 | 25 | 27 | 29 |
31 | 33 | 35 | 37 | 39 |
… | … | … | … | … |
(1)设T字框内处于中间且靠上方的数是整个数表当中从小到大排列的第n个数,请你用含n的代数式表示T字框中的四个数的和;
(2)若将T字框上下左右移动,框住的四个数的和能等于2020吗?如能,写出这四个数,如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形![]() 的边长是1米;
的边长是1米;
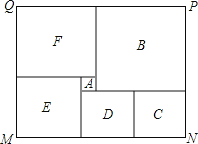
(1)若设图中最大正方形![]() 的边长是
的边长是![]() 米,请用含
米,请用含![]() 的代数式分别表示出正方形
的代数式分别表示出正方形![]() 的边长
的边长
(2)观察图形的特点可知,长方形相对的两边是相等的(即![]() ,
, ![]() )请根据以上结论,求出
)请根据以上结论,求出![]() 的值
的值
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
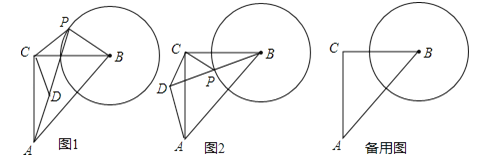
【题目】如图1.在△ABC中,∠ACB=90°,AC=BC=![]() ,以B为圆心、1为半径作圆,设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA、PD、PB.
,以B为圆心、1为半径作圆,设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA、PD、PB.
(1)求证:AD=BP;
(2)若DP与⊙B相切,则∠CPB的度数为 ;
(3)如图2,当B、P、D三点在同一条直线上时,求BD的长;
(4)BD的最小值为 ;BD的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“单词的记忆效率“是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.如图描述了某次单词复习中小华,小红小刚和小强四位同学的单词记忆效率y与复习的单词个数x的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )

A. 小华B. 小红C. 小刚D. 小强
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com