
分析 设O为正三角形ABC的外心(或内心),作OD⊥BC于D,连接OB,由正三角形的性质得出BD=$\frac{1}{2}$BC=$\frac{1}{2}$a,∠OBD=$\frac{1}{2}$∠ABC=30°,由三角函数求出r=OB=$\frac{BD}{cos30°}$,d=OD=$\frac{1}{2}$r,即可得出结果.
解答 解:如图所示:
设O为正三角形ABC的外心(或内心),作OD⊥BC于D,连接OB,
则BD=$\frac{1}{2}$BC=$\frac{1}{2}$a,∠OBD=$\frac{1}{2}$∠ABC=30°,
∴r=OB=$\frac{BD}{cos30°}$=$\frac{\frac{1}{2}a}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{3}$a,
d=OD=$\frac{1}{2}$r=$\frac{\sqrt{3}}{6}$a,
∴r=2d;
故答案为:$\frac{\sqrt{3}}{3}$a,$\frac{\sqrt{3}}{6}$a;r=2d.
点评 本题考查了正三角形的性质、三角形的外接圆半径、内切圆半径、三角函数;通过作辅助线解直角三角形求出r和d是解决问题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
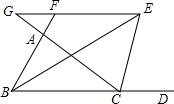 如图,在△ABC中,外角∠ACD的平分线与内角∠ABC的平分线相交于点E,过点E作BD的平行线分别交AB,AC边所在的直线于点F、G,则BF、CG、FG三条线段之间存在怎样的数量关系?请写出结论,并加以证明.
如图,在△ABC中,外角∠ACD的平分线与内角∠ABC的平分线相交于点E,过点E作BD的平行线分别交AB,AC边所在的直线于点F、G,则BF、CG、FG三条线段之间存在怎样的数量关系?请写出结论,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间t/s | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 速度v/(m/s) | 5 | 5+$\frac{1}{10}$ | 5+$\frac{4}{10}$ | 5+$\frac{9}{10}$ | 5+$\frac{16}{10}$ | 5+$\frac{25}{10}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
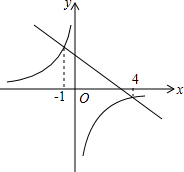 如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,不等式ax+b>$\frac{k}{x}$的解集为x<-1或0<x<4.
如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,不等式ax+b>$\frac{k}{x}$的解集为x<-1或0<x<4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com