[题目]如图.在△ABC中.已知AB=BC.∠B=120°.AB的垂直平分线交AC于点D.若AC=6.求AD的长．题目和参考答案——青夏教育精英家教网—

【题目】如图，在△ABC中，已知AB=BC，∠B=120°，AB的垂直平分线交AC于点D，若AC=6，求AD的长．

【答案】解：连接BD，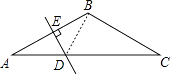
∵AB=BC，∠ABC=120°，
∴∠A=∠C= （180°﹣∠ABC）=30°，
∴DC=2BD，
∵AB的垂直平分线是DE，
∴AD=BD，
∴DC=2AD，
∵AC=6，
∴AD= ×6=2
【解析】连接BD，根据三角形的内角和定理和等腰三角形性质推出∠C=30°，根据含30°角的直角三角形性质得出DC=2BD，根据线段垂直平分线的性质推出AD=BD，即可求出答案．
【考点精析】通过灵活运用线段垂直平分线的性质和含30度角的直角三角形，掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半即可以解答此题．

练习册系列答案

中考123基础章节总复习测试卷系列答案

中考123中考复习必备系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】某个样本的频数分布直方图中一共有4组，从左至右的组中值依次为5，8，11，14，频数依次为5，4，6，5，则频率为0.2的一组为（）
A.6.5～9.5
B.9.5～12.5
C.8～11
D.5～8

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图，在矩形ABCD中，Ab=6cm，BC=8cm，对角线AC，BD交于点0．点P从点A出发，沿方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F．设运动时间为t（s）（0＜t＜6），解答下列问题：

（1）当t为何值时，△AOP是等腰三角形？

（2）设五边形OECQF的面积为S（cm2），试确定S与t的函数关系式；

（3）在运动过程中，是否存在某一时刻t，使S五边形S五边形OECQF：S△ACD=9：16？若存在，求出t的值；若不存在，请说明理由；

（4）在运动过程中，是否存在某一时刻t，使OD平分∠COP？若存在，求出t的值；若不存在，请说明理由．

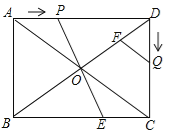
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】体育教师在操场上画100m的直跑道，如果画6条跑道，需要画__________条线段，这些线段的位置关系是__________

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上，OC=8，OE=17，抛物线与y轴相交于点A，抛物线的对称轴与x轴相交于点B，与CD交于点K．

（1）将矩形OCDE沿AB折叠，点O恰好落在边CD上的点F处．

①点B的坐标为（、），BK的长是，CK的长是；

②求点F的坐标；

③请直接写出抛物线的函数表达式；

（2）将矩形OCDE沿着经过点E的直线折叠，点O恰好落在边CD上的点G处，连接OG，折痕与OG相交于点H，点M是线段EH上的一个动点（不与点H重合），连接MG，MO，过点G作GP⊥OM于点P，交EH于点N，连接ON，点M从点E开始沿线段EH向点H运动，至与点N重合时停止，△MOG和△NOG的面积分别表示为S1和S2，在点M的运动过程中，S1S2（即S1与S2的积）的值是否发生变化？若变化，请直接写出变化范围；若不变，请直接写出这个值．

温馨提示：考生可以根据题意，在备用图中补充图形，以便作答．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某品牌汽车生产厂为了占领市场提高销售量，对经销商采取销售奖励活动，在2014年10月前奖励办法以下表计算奖励金额，2014年10月后以新奖励办法执行．某经销商在新奖励办法出台前一个月共售出某品牌汽车的A型和B型共413台，新奖励办法出台后的第一个月售出这两种型号的汽车共510台，其中A型和B型汽车的销售量分别比新奖励办法出台前一个月增长25％和20％．2014年10月前奖励办法：

销售量（x台）	每台奖励金额（元）
0＜x≤ 100	200
100＜x≤300	500
x＞300	1000

（1）在新办法出台前一个月，该经销商共获得奖励金额多少元？
（2）在新办法出台前一个月，该经销商销售的A型和B型汽车分别为多少台？
（3）若A型汽车每台售价为10万元，B型汽车每台售价为12万元．新奖励办法是：每销售一台A型汽车按每台汽车售价的给予奖励，每销售一台B型汽车按每台汽车售价的给予奖励．新奖励办法出台后的第二个月，A型汽车的销售量比出台后的第一个月增加了；而B型汽车受到某问题零件召回的影响，销售量比出台后的第一个月减少了，新奖励办法出台后的第二个月该经销商共获得的奖励金额355680元，求的值．