
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
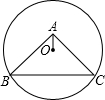 如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{13}$ | C. | 4 | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
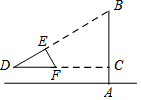 如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )
据新华网消息,2016年6月20日,使用中国自主芯片制造的超级计算机“神威太湖之光”以浮点运算速度每秒930000000亿次登上全球500强榜首,数字930000000用科学记数法可表示为( )| A. | 9.3×108 | B. | 93×107 | C. | 0.93×109 | D. | 9.3×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
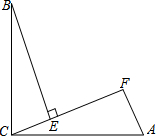 如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.
如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 250×104 | B. | 2.5×105 | C. | 2.5×106 | D. | 2.5×107 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com