
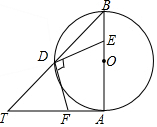
 如图,AB是⊙O的直径,AT=AB,∠ABT=45°.
如图,AB是⊙O的直径,AT=AB,∠ABT=45°.分析 (1)求出∠BAT=90°,根据切线的判定得出即可;
(2)证△DFE≌△DEA,求出AE=TF=4,根据勾股定理得出关于R的方程,求出即可.
解答 (1)证明:∵在△BAT中,AT=AB,∠ABT=45°,
∴∠T=∠ABT=45°,
∴∠BAT=90°,
即BA⊥AT,
∵AB过圆心O,
∴AT是⊙O的切线;
(2)解:
连接AD,OD,
∵AB为直径,
∴∠ADB=90°,
∵AB=AT,
∴DT=BD,
∵∠BAT=90°,
∴DT=BD=AD,
∵∠BAT=90°,DE⊥DF,
∴∠DFA+∠DEA=360°-90°-90°=180°,
∵∠DFA+∠DFT=180°,
∴∠DFT=∠DEA,
∵∠TDA=∠ADB=∠BAT=90°,
∴∠DTA+∠DAT=90°,∠DAT+∠DAE=90°,
∴∠T=∠DAE,
在△DFT和△DEA中
$\left\{\begin{array}{l}{∠T=∠DAE}\\{∠DFT=∠DEA}\\{TD=DA}\end{array}\right.$
∴△DFT≌△DEA,
∴DF=DE=$\sqrt{10}$,AE=FT=4,
设⊙O的半径为R,
在Rt△DOE中,DE2=DO2+OE2,
($\sqrt{10}$)2=R2+(4-R)2,
解得:R=1或3,
∵E在OB上,AE=4,
∴当R=1时,AB=2<4,此时不符合舍去,
即⊙O的半径为3.
点评 本题考查了切线的判定,全等三角形的性质和判定,勾股定理,等腰直角三角形的性质等知识点,能综合运用性质和定理进行推理是解此题的关键,综合性比较强,难度偏大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
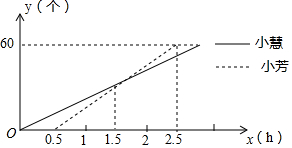 某厂要加工一批新型零件,让小慧和小芳每人试加工60个,小慧一上班就开始试加工,小芳接受半小时培训后再开始试加工,如图所示为小慧和小芳试加工过程中加工的零件数y(个)与加工时间x(h)之间的函数图象,请根据图象所提供的信息解答下列问题:
某厂要加工一批新型零件,让小慧和小芳每人试加工60个,小慧一上班就开始试加工,小芳接受半小时培训后再开始试加工,如图所示为小慧和小芳试加工过程中加工的零件数y(个)与加工时间x(h)之间的函数图象,请根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
| 批发价(元/kg) | 3.6 | 5.4 | 8 | 4.8 |
| 零售价(元/kg) | 5.4 | 8.4 | 14 | 7.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
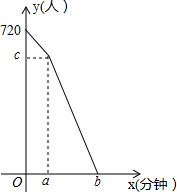 五一假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有720人排队检票,检票开始后,仍有旅客继续前来排队检票进站,设旅客按固定的速度增加,检票口检票的速度也是固定的,检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人,已知检票的前a分钟只开放了2个检票口,a分钟后又开放了2个检票窗口,候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.(b>a)
五一假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有720人排队检票,检票开始后,仍有旅客继续前来排队检票进站,设旅客按固定的速度增加,检票口检票的速度也是固定的,检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人,已知检票的前a分钟只开放了2个检票口,a分钟后又开放了2个检票窗口,候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.(b>a)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平时检测成绩 | 平时检测平均成绩 | |||||
| 检测1 | 检测2 | 检测3 | 检测4 | 检测5 | ||
| 李刚 | 90 | 80 | 90 | 80 | 85 | |
| 王强 | 75 | 90 | 80 | 85 | 95 | 85 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com