
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 先利用代入消元法求出点的坐标,再根据向左平移横坐标减求出平移后的点的坐标,然后根据各象限内点的坐标特征解答.
解答 解:$\left\{\begin{array}{l}{y=-x+2①}\\{y=x-1②}\end{array}\right.$,
①代入②得,-x+2=x-1,
解得x=$\frac{3}{2}$,
将x=$\frac{3}{2}$代入②得,y=$\frac{3}{2}$-1=$\frac{1}{2}$,
所以,方程组的解是$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{1}{2}}\end{array}\right.$,
所以,点的坐标为($\frac{3}{2}$,$\frac{1}{2}$),
∵点(x,y)向左平移3个单位,
∴平移后的点的横坐标为$\frac{3}{2}$-3=-$\frac{3}{2}$,
∴平移后的点的坐标为(-$\frac{3}{2}$,$\frac{1}{2}$),在第二象限.
故选B.
点评 本题考查了坐标与图形变化-平移,解二元一次方程组,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
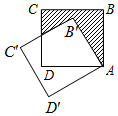 如图,边长为3的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
如图,边长为3的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )| A. | 6+3$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 1-$\frac{\sqrt{3}}{3}$ | D. | 9-3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
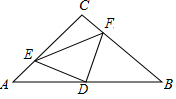 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,E,F两点分别在AC,BC边上运动 (点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,E,F两点分别在AC,BC边上运动 (点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠ABC,∠ACB的平分线相交于点O,下而结论中正确的是( )
如图,△ABC中,∠ABC,∠ACB的平分线相交于点O,下而结论中正确的是( )| A. | ∠1>∠2 | B. | ∠1=∠2 | C. | ∠1<∠2 | D. | ∠1=2∠2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com