
 如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,CM=4.在射线CF上取一点A,连接AM并延长交射线OE于点B,作BD⊥OF于点D.
如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,CM=4.在射线CF上取一点A,连接AM并延长交射线OE于点B,作BD⊥OF于点D.分析 (1)由于∠MCA=∠BDO=Rt∠,所以△AMC和△BOD相似时分两种情况:①△AMC∽△BOD;②△AMC∽△OBD.则两种情况都可以根据相似三角形对应边的比相等及tan∠EOF=2列出关于AC的方程,解方程即可求出AC的长度;
(2)先由MC∥BD,得出△AMC∽△ABD,根据相似三角形对应边的比相等及三角形中位线的性质求出BD=2MC=8,OD=4,CD=8,AC=CD=8,再利用SAS证明△AMC≌△BOD,得到∠CAM=∠DBO,根据平行线的性质及三角形内角和定理求出∠ABO=90°,进而得出△ABO为直角三角形.
解答 解:(1)∵∠MCA=∠BDO=90°,
∴△AMC和△BOD中,C与D是对应点,
∴△AMC和△BOD相似时分两种情况:
①当△AMC∽△BOD时,$\frac{AC}{MC}$=$\frac{BD}{DO}$=tan∠EOF=2,
∵MC=4,∴$\frac{AC}{4}$=2,即AC=8,
②当△AMC∽△OBD时,$\frac{MC}{AC}$=$\frac{BD}{DO}$=tan∠EOF=2,
∵MC=4,∴$\frac{4}{AC}$=2,即AC=2,
∴当AC的长度为2或8时,△AMC和△BOD相似;
(2)△AOB为直角三角形.
证明:∵MC∥BD,
∴△AMC∽△ABD.
∴$\frac{MC}{BD}$=$\frac{AM}{AB}$=$\frac{AC}{AD}$,
∠AMC=∠ABD.
∵M为AB中点,
∴C为AD中点,BD=2MC=8.
∵tan∠EOF=2,
∴OD=4,
∴CD=OC-OD=8,
∴AC=CD=8,
在△AMC与△BOD中,
$\left\{\begin{array}{l}{AC=BD=8}\\{∠ACM=∠BDO=90°}\\{CM=DO=4}\end{array}\right.$,
∴△AMC≌△BOD(SAS),
∴∠CAM=∠DBO,∠NAC=∠O,
∴∠ABO=∠ABD+∠DBO=∠AMC+∠CAM=90°,AB=BO,
∴△AOB为等腰直角三角形.
点评 本题主要考查了相似三角形的判定与性质,锐角三角函数的定义,三角形中位线定理,综合性较强,有一定难度.进行分类讨论是解决第一问的关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:填空题
 如图,∠AOB=30°,点M、N分别是射线OA、OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,四边形PMON的面积为36$\sqrt{3}$-54.
如图,∠AOB=30°,点M、N分别是射线OA、OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,四边形PMON的面积为36$\sqrt{3}$-54.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
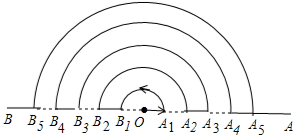 点O在直线AB上,点A1、A2、A3,…在射线OA上,点B1、B2、B3,…在射线OB上,图中的每一个实线段和虚线段的长均为一个单位长度,一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度,按此规律,动点M到达B1处所需时间为π+1秒,则动点M到达A101点处所需时间为(101+5050π)秒.
点O在直线AB上,点A1、A2、A3,…在射线OA上,点B1、B2、B3,…在射线OB上,图中的每一个实线段和虚线段的长均为一个单位长度,一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度,按此规律,动点M到达B1处所需时间为π+1秒,则动点M到达A101点处所需时间为(101+5050π)秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
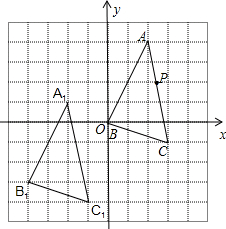 在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1.
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com