
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案科目:初中数学 来源: 题型:
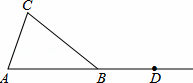
如图,在△ABC中,AB=BC,点点D在AB的延长线上.
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作∠CBD的平分线BM;
②作边BC上的中线AE,并延长AE交BM于点F.
(2)由(1)得:BF与边AC的位置关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进 、
、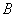 两种型号的低排量汽车,其中
两种型号的低排量汽车,其中 型汽车的进货单价比
型汽车的进货单价比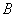 型汽车的进货单价多2万元;花50万元购进
型汽车的进货单价多2万元;花50万元购进 型汽车的数量与花40万元购进
型汽车的数量与花40万元购进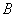 型汽车的数量相同.销售中发现
型汽车的数量相同.销售中发现 型汽车的每周销量
型汽车的每周销量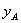 (台)与售价
(台)与售价 (万元/台)满足函数关系
(万元/台)满足函数关系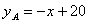 ,
,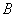 型汽车的每周销量
型汽车的每周销量 (台)与售价
(台)与售价 (万元/台)满足函数关系
(万元/台)满足函数关系
(1)求 、
、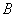 两种型号的汽车的进货单价;
两种型号的汽车的进货单价;
(2)已知 型汽车的售价比
型汽车的售价比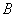 型汽车的售价高2万元/台.设
型汽车的售价高2万元/台.设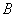 型汽车售价为
型汽车售价为 万元/台,每周销售这两种车的总利润为
万元/台,每周销售这两种车的总利润为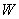 万元,求
万元,求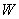 与
与 的函数关系式,
的函数关系式,  、
、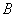 两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
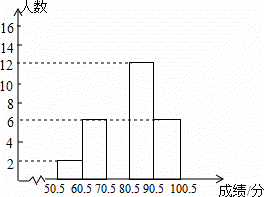
某公司为了解员工对“六五”普法知识的知晓情况,从本公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
| 组别 | 分数段/分 | 频数/人数 | 频率 |
| 1 | 50.5~60.5 | 2 | a |
| 2 | 60.5~70.5 | 6 | 0.15 |
| 3 | 70.5~80.5 | b | c |
| 4 | 80.5~90.5 | 12 | 0.30 |
| 5 | 90.5~100.5 | 6 | 0.15 |
| 合计 | 40 | 1.00 |
(1)表中a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
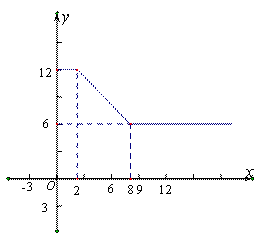
某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,B类杨梅深加工再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位∶万元/吨)与销售数量x(x≥2)(取位∶吨)之间的函数关系式如图,B类杨梅深加工总费用s(单位:万元)与加工数量t(单位∶吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)直接写出A类杨梅平均销售价格y与销售量x这间的函数关系式.
(2)第一次,该公司收购了20吨杨梅,其中A类杨梅x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收人-经营总成本).
①求w关于x的函数关系式
②若该公司获得了30万元毛利润,问∶用于直销的A类杨梅有多少吨?
(3)第二次该公司准 备投人132万元资金,请设计-种经营方案,使公司获得最大毛利润,并求出最大毛利润.
备投人132万元资金,请设计-种经营方案,使公司获得最大毛利润,并求出最大毛利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com