
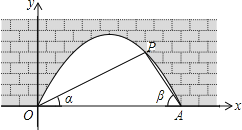
【题目】图中是抛物线拱桥,P处有一照明灯,点P到水面OA的距离为![]() ,从O、A两处观测P处,仰角分别为
,从O、A两处观测P处,仰角分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为
,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为![]() .
.
![]() 求抛物线方程,并求抛物线上的最高点到水面的距离;
求抛物线方程,并求抛物线上的最高点到水面的距离;
![]() 水面上升1m,水面宽多少
水面上升1m,水面宽多少![]() 取
取![]() ,结果精确到
,结果精确到![]() ?
?
【答案】(1)故抛物线方程为![]() ,抛物线上的最高点到水面的距离2m;
,抛物线上的最高点到水面的距离2m;
(2)水面宽约为![]() .
.
【解析】
(1)如图过点P作![]() 于H,求出
于H,求出![]() 中OH的长得到P点坐标,再求出
中OH的长得到P点坐标,再求出![]() 中AH长得到A点坐标为(4,0),所以可设抛物线解析式为
中AH长得到A点坐标为(4,0),所以可设抛物线解析式为![]() ,然后将P点坐标代入求解得到抛物线解析式,然后求出顶点坐标即可得到答案;
,然后将P点坐标代入求解得到抛物线解析式,然后求出顶点坐标即可得到答案;
(2)将y=1代入抛物线解析式中求解得到x的值,然后计算出水面宽即可.
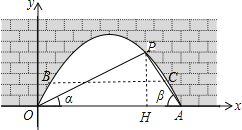
(1)过点P作![]() 于H,如图.
于H,如图.
在![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() ,
,
在![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∴点A坐标为(4,0),
过点![]() ,
,![]() 的抛物线的解析式可设为
的抛物线的解析式可设为![]() ,
,
![]() 在抛物线
在抛物线![]() 上,
上,
![]() ,
,
解得![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() =
=![]() ,
,
∴抛物线的顶点坐标为(2,2),
则抛物线上的最高点到水面的距离2m,
故抛物线方程为![]() ,抛物线上的最高点到水面的距离2m;
,抛物线上的最高点到水面的距离2m;
(2)若水面上升1m后到达BC位置,如图,
当![]() 时,
时,![]() ,
,
解得![]() ,
,![]() ,
,
![]() .
.
故水面宽约为![]() .
.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠BAC=100°,则∠EAG=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于A、B两点,其中点A的坐标为
与x轴交于A、B两点,其中点A的坐标为![]() ,抛物线的顶点为P.
,抛物线的顶点为P.
![]() 求b的值,并求出点P、B的坐标;
求b的值,并求出点P、B的坐标;
![]() 在x轴下方的抛物线上是否存在点M,使
在x轴下方的抛物线上是否存在点M,使![]() ≌
≌![]() ?如果存在,请直接写出点M的坐标;如果不存在,试说明理由.
?如果存在,请直接写出点M的坐标;如果不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有4个小球,分别标有数字1,2,3,4;这些小球除所标数字不同外,其余完全相同,甲乙两人每次同时从袋中各随机摸出一个小球,记下球上的数字,并计算它们的积.
![]() 请用画树状图或列表的方法,求两数积是8的概率;
请用画树状图或列表的方法,求两数积是8的概率;
![]() 甲乙两人想用这种方式做游戏,他们规定,当两数之积是偶数时,甲得1分,当两数之积是奇数时,乙得3分,你认为这个游戏公平吗?请说明理由,若你认为不公平,请修改得分规则,使游戏公平.
甲乙两人想用这种方式做游戏,他们规定,当两数之积是偶数时,甲得1分,当两数之积是奇数时,乙得3分,你认为这个游戏公平吗?请说明理由,若你认为不公平,请修改得分规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,射线OA是第一象限的角平分线,点C(11,5),E,F分别是射线OA和x轴正半轴的动点,那么FE+FC的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
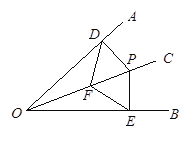
【题目】如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
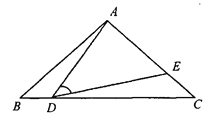
【题目】如图,在△ABC中,AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线段BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE.
(1)运动 秒时,AE=![]() DC(不必说明理由)
DC(不必说明理由)
(2)运动多少秒时,∠ADE=90°-![]() ∠BAC,并请说明理由;
∠BAC,并请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
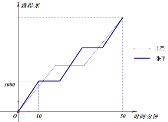
【题目】“绿带城中挂,人在画中游”,张平和王亮同学周末相约骑行于“步移景异,心旷神怡”的温江田园绿道,他们从同一地方同时骑自行车出发(骑行过程中速度保持不变),最后同时到达了同一个地方. 如图刻画了他们离出发点的路程(单位:米)与出发后的时间(单位:分钟)之间的关系. 已知张平中途两次休息时间相同,三段骑行时间也分别相同;王亮中途休息一次,两段骑行时间相同. 张平总的休息时间比王亮的休息时间多![]() 分钟. 请结合图中信息解答下列问题:
分钟. 请结合图中信息解答下列问题:
(1)在这次骑行活动中,他们的骑行路程都是多少米?
(2)求出张平和王亮的骑行速度分别是多少米/分钟?
(3)求出王亮出发后第一次追上张平的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com