
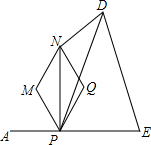
 如图,已知线段AE=10,点P是线段AE上的动点,以AP长为边长作菱形PMNQ,已知该菱形的一个锐角∠MPQ=60°,且对角线NP⊥AE,△PED是以PE为底的等腰三角形,则△PND的面积的最大值是$\frac{25\sqrt{3}}{4}$.
如图,已知线段AE=10,点P是线段AE上的动点,以AP长为边长作菱形PMNQ,已知该菱形的一个锐角∠MPQ=60°,且对角线NP⊥AE,△PED是以PE为底的等腰三角形,则△PND的面积的最大值是$\frac{25\sqrt{3}}{4}$. 分析 作DH⊥PN于H,DF⊥PE于F,连结MQ交PN于O点,如图,设PA=x,则PM=x,PE=10-x,根据菱形的性质得OP=ON,PN⊥MQ,∠MPO=$\frac{1}{2}$∠MPQ=30°,在Rt△OPM中利用三角函数可求出PO=$\frac{\sqrt{3}}{2}$x,则PN=2PO=$\sqrt{3}$x,再证明四边形PFDH为矩形得DH=PF,接着根据等腰三角形的性质得PF=EF=$\frac{1}{2}$(10-x),然后根据三角形面积公式得到S△PND=$\frac{1}{2}$•$\sqrt{3}$x•$\frac{1}{2}$(10-x),最后利用二次函数的性质求S△PND的最大值.
解答 解:作DH⊥PN于H,DF⊥PE于F,连结MQ交PN于O点,如图, 设PA=x,则PM=x,PE=10-x,
设PA=x,则PM=x,PE=10-x,
∵四边形PMNQ为菱形,
∴OP=ON,PN⊥MQ,∠MPO=$\frac{1}{2}$∠MPQ=30°,
在Rt△OPM中,∵cos∠MPO=$\frac{OP}{PM}$,
∴PO=x•cos30°=$\frac{\sqrt{3}}{2}$x,
∴PN=2PO=$\sqrt{3}$x,
∵PN⊥AE,DF⊥PE,DH⊥HP,
∴四边形PFDH为矩形,
∴DH=PF,
∵DP=DE,DF⊥PE,
∴PF=EF=$\frac{1}{2}$PE=$\frac{1}{2}$(10-x),
∴S△PND=$\frac{1}{2}$•PN•DH=$\frac{1}{2}$•$\sqrt{3}$x•$\frac{1}{2}$(10-x)
=-$\frac{\sqrt{3}}{4}$(x-5)2+$\frac{25\sqrt{3}}{4}$,
当x=5时,S△PND的值最大,最大值为$\frac{25\sqrt{3}}{4}$.
故答案为$\frac{25\sqrt{3}}{4}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了三角形面积公式和二次函数的性质.


科目:初中数学 来源: 题型:解答题
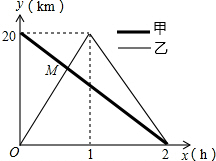 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
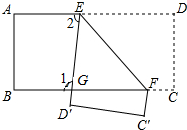 如图,把一张长方形纸片ABCD沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上.
如图,把一张长方形纸片ABCD沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
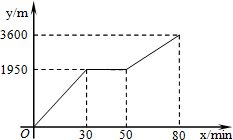 “五一”黄金周期间,甲乙两人相约去宾县二龙山游玩,两人到山脚下缆车起点,甲乙准备上山顶游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合,已知乙从山脚下缆车起点走到山顶缆车终点的路程是缆车从山脚下缆车起点到山顶缆车终点的线路长的2倍.由于乘坐缆车的人比较多,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min,设乙出发x min后行走的路程为y m,图中的折线表示乙在整个过程中y与x的函数关系,下列问题叙述正确的个数有( )
“五一”黄金周期间,甲乙两人相约去宾县二龙山游玩,两人到山脚下缆车起点,甲乙准备上山顶游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合,已知乙从山脚下缆车起点走到山顶缆车终点的路程是缆车从山脚下缆车起点到山顶缆车终点的线路长的2倍.由于乘坐缆车的人比较多,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min,设乙出发x min后行走的路程为y m,图中的折线表示乙在整个过程中y与x的函数关系,下列问题叙述正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在高5m的房顶A处望一楼的底部D,视线刚好过小树的顶端E,又从楼顶C处望房顶部B,视线也正好过小树的顶端E,测得小树高4m,求楼高CD.
如图,在高5m的房顶A处望一楼的底部D,视线刚好过小树的顶端E,又从楼顶C处望房顶部B,视线也正好过小树的顶端E,测得小树高4m,求楼高CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )
小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )| A. | 掷一枚质地均匀的硬币,正面朝上的概率 | |
| B. | 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率 | |
| C. | 从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率 | |
| D. | 任意买一张电影票,座位号是2的倍数的概率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com